AH
TALENT)THIRTEEN     Problem D-9
       TRREEEK
        IKANAAN
        NTNRNXE
         HIKIRE

Table of Contents

Introduction
A brief history of cryptarithms

Part 1: General Solving Techniques
1. Search for Zero
2. Identifying One and Nine
3. Greater Than, Less Than, and Consecutive Digits
4. Multiplication Principles: Identities and Odd and Even Numbers
5. Leading Digit Analysis
  Second Digit Analysis
  Internal Zeros and Split Partial Products
  Multiplying Out
6. Extra Additions: The Hubbuber Trick
7. Double and Triple Table Matching

Part 2: Solving Specific Problem Types and Other Advanced Methods
8. Interlocking Equations
9. Double-Key Problems
10. Magic Squares
11. Additions With More Than Two Addends
12. Single-Digit Multiplications and Internal Multiplication
13. Topless Divisions and Related Puzzles
14. Special Form Tables
15. Crotalus Rectangles

Part 3: Other Bases
Multiplication in Other Bases
Multiplicative Structures
Roots in Other Bases

Part 4: Construction Techniques
Finding Cryptarithms via Computer Search
Exploring Minimum Ideals
Interlocking Equation Formulas
Magic Squares
Computing LDA Tables
Ideal Doubly True Cryptarithms (besides Additions)
A note on combinations and computer solving

Appendix 1: An Annotated Bibliography

Appendix 2: Supplementary Problems
Additions
  Thematic Additions
  Fibonacci Sequences
  Extra Long Additions
Divisions
Interlocking Equations
Double-Key Divisions
Multiplications
  Single Digit Multiplications
  Double-Key
  Topless and Bottomless
  Ideal Doubly True
Magic Squares
Square and Higher Roots
Topless Divisions
Challenge Problems
  Wodehouse Alphacipher

Appendix 3: Solving Hints and Walkthroughs for Selected Puzzles

Appendix 4: Tables
Special Form Tables
LDA Tables

Appendix 5: Solutions
Appendix 6: Examples of Hidden Cryptarithms
Appendix 7: Glossary

Introduction

Portions of this booklet were originally published in the Cryptophile Cryptofile column of WGR8, July 1988, pp. 5-11, and in a few later issues.   A special issue of WGR devoted to cryptarithms was intended, but never published (problem D-9 at the top was meant to appear on the cover of WGR13).  Almost all the puzzles herein are my own compositions; the few exceptions are explicitly credited.   Three of the puzzles appeared in the online game journal The Games Cafe, which ran for a few months in 2000 (even the Internet Archive couldn't locate the originals).

A cryptarithm is a logic puzzle in which arithmetic calculations are disguised by replacing the digits with letters or other symbols, the object being to discover the original digits.   [Essentially, a cryptarithm is a simple substitution cipher in which the hidden message is an arithmetic problem.]    A given letter must represent the same digit each time it occurs in the puzzle.  In standard cryptarithms, a digit must be represented by the same letter each time it occurs.   Leading zeros are almost never permitted; if they are permitted in a particular problem, this fact must be clearly stated.  Solving cryptarithms requires the use of logic and simple arithmetic (and sometimes light algebra), but cryptarithms can range from very simple to excruciatingly difficult.  Cryptarithms are composed on all of the usual arithmetic operations.  Additions are most common, but divisions and multiplications are also frequent.  Subtractions are sometimes seen, but can be recast as additions for solving purposes (they also occur as part of long divisions).   Square roots are not often seen, outside of the cryptarithm page in The Cryptogram (which also features cube roots, and occasionally higher roots, equations involving powers and fractions (usually seen as specials: unusual or difficult problems), and magic squares.  Most cryptarithms are composed in ordinary base 10 (decimal) arithmetic, but base 11 (undecimal) and base 12 (duodecimal) appear regularly.  Larger bases up to 16 (hexadecimal), and sometimes smaller bases such as 7, 8, and 9 are occasionally seen.   Cryptography regularly published sets of interlocking equations (combining additions, subtractions, multiplications, and divisions); they occasionally could be found in other publications like Four-Star Puzzler.

Among the various operations, problems using square roots are easiest to solve, because it is usually possible to determine the value of several letters very quickly.  Divisions are next easiest, because they contain a number of different multiplications and additions, providing many clues.   Interlocking equations are also generally easy.   Multiplications, and additions in which only two numbers are added, tend to be of medium difficulty.  Although multiplications with only two digit multipliers are sometimes easy because the additions have only two addends, multiplications generally get easier as the multiplier gets longer because of the large number of partial products, and addition clues (except for the first few columns at both ends) are not usually needed.   Additions with three or more addends are the most difficult of the most commonly seen types.  

A goal of the composer in many cryptarithm puzzles is for as many of its elements as possible to consist of actual words.  I call such an element coherent; the division D-9 above has coherent dividend, divisor, and quotient.   Puzzles where all of the elements are coherent is often referred to as an alphametic (a term coined in 1955 by J.A.H. Hunter): usually either the words are thematic, or make a sensible phrase.   These are generally additions; making completely coherent multiplications and divisions is much more difficult.   Cryptarithms in The Cryptogram and some other publications are usually composed so that the letters representing each digit spell out a word or words (such as JOURNALIST or ZERO TULIPS; this is called the keyword) when arranged in the order 0-9 (as above), 9-0, 1-0 (1234567890), or 0-1.   Using keywords sometimes renders them vulnerable to solution (by lazy solvers) by anagramming instead of normal methods (I rarely use single word keys for this reason).   Clever keywords serve as a kind of reward to the solver, especially if the keyword is thematically related to words in the puzzle.   In this booklet, I try to provide a keyword for every puzzle, though most are in mixed numerical order (the more coherent a puzzle, the harder it is to make a keyword in one of the fixed orders).

Like other kinds of logic puzzles, cryptarithms should only have a single solution, although this principle is not always followed.   An ideal cryptarithm is defined as one which uses every digit in the base being used (e.g. 10 in decimal), only one letter represents each digit, the letters representing each digit are distinct, and there is only one solution.   Nearly all of the puzzles in this booklet are ideal.

Many published alphametics have multiple solutions (sometimes only interchangeable digits, but often completely independent solutions).  Usually some constraint on one or more of the digits (or entire numbers), stating that they must be prime, even, odd, etc. (less satisfactory are problems asking for the largest or smallest solution). If the cryptarithm has only nine digits, the missing digit might be specified.   Another method might be to show the value of one of the carries.

An exception to the usual one letter/one digit rule is the double-key cryptarithm.  This uses two separate keywords, one conventionally written in capitals and the other in lower case letters.  As it occurs in The Cryptogram, it is usually a division problem, though other operations have been used.  This is probably the hardest category of regular cryptarithms, and is rarely seen outside of The Cryptogram (and today, far less often than in years gone by).

Doubly true cryptarithms are those in which a true arithmetic problem is spelled out in words so that it makes a valid cryptarithm as well.  Excellent examples of ideal doubly true (idt) cryptarithms can be found in Stephen Kahan's book Have Some Sums To Solve and its two sequels, as well as in The Journal of Recreational Mathematics.   A variant of this is the digimetic, in which a correct addition expressed in digits represents another correct addition, so that none of the corresponding digits in the two additions are the same (see puzzle A-200).  This puzzle was named and championed in JRM by Sidney Kravitz.   A remarkable example is alphametic number 1544 from JRM (see Bibliography).

A separate category of cryptarithms is a type in which most or all of the digits are removed and replaced by identical nulls (marks such as dots, dashes, or asterisks).  These marks ordinarily may represent any digit, but sometimes restrictions are placed on them. This puzzle has been called by various names, including skeleton puzzle, arithmetical restoration, and dotty problem (a colorful term used by Nob Yoshigahara and his Japanese colleagues in Puzzletopia), but we will use the generic term hidden cryptarithm.  These are nearly always divisions or multiplications.  In its purest form, the hidden cryptarithm does not contain any letters, and the values of only a few digits are shown.  A common restriction in such puzzles is that no asterisk may represent a digit which is shown, but not every construction follows that rule.  There are also hybrids (partially hidden) which combine letters representing specific digits, and nulls representing any digit.   Some multiplication and division alphametics are of this type.

Hidden cryptarithms generally range from relatively easy to extremely hard, and require very different techniques from standard letter cryptarithms; the hardest are among the toughest of all cryptarithms to solve (the rarest and most difficult are completely hidden cryptarithms in which no digits or letters are seen, only nulls; the only information thus available to the solver is the length of each element).   We will not look at detailed techniques of solving hidden cryptarithms here, but the Bibliography gives a number of sources which include problems with detailed solutions, which will demonstrate some of the techniques involved, including factorization.   We give a few example puzzles in Appendix 6.

The annotated bibliography in Appendix 1 has details on books and magazines with substantial content on cryptarithms, particularly on solving and construction methods.

Note: Some sources, including The Cryptogram, publish cryptarithms in a linear format (the division at the beginning of this booklet might appear as THIRTEEN / TALENT = AH; - TRREEEK = IKANAAN; - NTNRNXE = HIKIRE).  That practice saves little if any space, requires each problem to be recopied (a process prone to error), and occasionally leads to ambiguities (when partial products are missing) which must be worked out.  The first column in The Cryptogram which used linear format (February 1938), published four puzzles which took up the bottom half of page 13, using 35 columns of horizontal space and at least 26 vertical lines.  I was able to format this comfortably on graph paper within a box of 24 x 24 squares; I could have fit six medium-sized puzzles in that space.  The only advantage I can think of for the linear format is a very sophisticated solving/checking program which could read a single line of input; the only program I know that can do this is CryptoCrack.  All of the puzzles here are formatted as standard multiline calculations.   We use x for multiplication (and / for division in Interlocking Equation puzzles).   

A brief history of cryptarithms 

Part 1: General Solving Techniques

1. Search for Zero

One useful technique in solving is to try to find the letter which represents zero.   Barring a positive indicator that a letter represents zero (a missing partial product or an addition indicating zero; examples 1-5 below), it is often worthwhile to seek zero by a process of elimination.  [For the moment we will assume normal base 10 arithmetic. We will examine other bases in Part 4.]    Below left are the principal indicators that a letter cannot represent zero:

        a.....b      
     x     accc     
       a.....de     
      a......d      
     a......e         
    a......e           
    af........e          

   General Framework     
     Multiplication  

a: Letters in positions marked a are never zero: leading digits, by convention, are not permitted to be zero.
b: The letter in position b is not zero unless all of the partial products also end in b (Example 4, above right), and it is obvious from the tens column addition that the second partial product ends in 0.  If all of the partial products end in zero, but the multiplicand ends in a different letter Z (Example 5, above right), Z must equal 5.
c: Other digits in the multiplier can only equal zero if one of the partial products is missing (Example 3).
d: Neither of the tens-column digits can be zero unless the sum is equal to the other letter (Examples 1 and 2), or all three are the same letter.
e: If b is not zero, the units digit (rightmost digit of both the first partial product and the sum (full product)) can be zero only if the multiplicand ends in 5 and the multiplier ends in an even number, or vice versa.  The same is true of the rightmost digits of the third and successive partial products.  If more than one non-identical partial product ends in zero, the multiplicand must end in 5, and all of the corresponding digits of the multiplier must be even.  The partial products not ending in zero must all end in 5, with odd corresponding digits in the multiplier.  In example 5, g and h are odd and i and j are even.
f: The second-leftmost digit of the product cannot be zero if there is no carry to the leftmost column of the addition.
g: The square of a non-zero digit is never zero.

       .......           .......           .......           ......X          ......Z     
    x     ....        x     ....        x     .X..        x     ....       x     ghij
      ......X.          ......Y.          ........          ......YX         ......YX
     .......Y          .......X          ........          .......X         .......X
    ........          ........         ........           .......X         .......Z
   ........          ........          ...........       .......X         .......Z    
   .........Y.       .........Y.                         .........Y.      .........Y.

  AB....       AC.....        A....       E.......         ...B...               ....A             ..A..
- AC....     +  D.....     + DB....      -DB......       + ...A...             + ....B           + ..B..
   D....       AB.....       E.....        A......         ...C...               ....C             ..C..

B is not 0    B is not 0     B is not 0    B is not 0     B is not 0       A and B are not 0     If C = 1,
                                                        if [AD] or [EC]                       either A nor B is 0

The exceptional case below sometimes occurs in multiplications with a multiplier of at least three digits.  C + D + (carry) = E, carrying to [AB], is possible with D = 0 only if the carry is 2, C = 9, and E = 1.  But 9 can be the leading digit of C... only if it is a short product.   See M-205 for an example.

     .....
    C....    
 + AD...    
   BE.....   

A digit repeated in adjacent columns

When a letter is an addend in two adjacent columns, each with three unlike letters, it cannot be zero.   In the examples below, if B = 0, the addition on the right gives [CE], but then there is no carry to the addition to its left (see M-154 for an example, which also uses two other techniques to eliminate three of four initial candidates).  The same principle also prevents B from being 9, as there will then be a carry which makes B = 9 impossible in the next column to the left.

In section 4 we will look at ways to sort letters into odd and even groups.  Any letter we can put in the odd group can also be ruled out as zero (a famous problem by Bubbles, C-3 in The Cryptogram of October-November 1949, allows the letters to be sorted quickly into five even and five odd, with two of the three possibilities for zero falling into the odd group, leaving the only even candidate as zero).

Breakdown by Cases

If there are only a few cases, or easy equivalences can be made knowing which letter equals zero, we can break down the problem and solve it case by case (this is a useful technique for very difficult additions, such as A-8 and A-14, and divisions with a single digit quotient, like D-36, and D-39; see M-84 and M-166 for more examples).   M-421 has three possibilities, two of which can be eliminated quickly.  M-18, M-116, and M-155 combine search for zero with an identity multiplication we will see in section 4.

2. Identifying One and Nine

One

    B...        A...       ...B       B....      ...B       ...B...
 x  ...C    x   ...B    x  ...A     + C....    + ...B     + ...A...
    A...       C....      ....C       A....      ...A       ...B...

A cannot equal 1 if it is the leading digit of a short product (Example 1), or if it is the leading digit of a multiplicand which has a long product with a different leading digit (Example 2, where C < A), or if it is a multiplier digit with a product different from the multiplicand (example 3).   A cannot be 1 if it is the leftmost sum of an addition with no carry (we saw this above with zero: A must be at least 3).   A cannot be 1 if it is clearly even (e.g. Example 5), or if is part of an identity addition (Example 6).

          A...              CDEF                   ...A             B...
    x     ...B        x     ...A             x     BCDE           + C...
          B...              CDEF                  ....E            A....
     ........          ........                  ....D    
    ........          ........                  ....C     
   ........          ........                  ....B       
   ...........       ...........               ........          

A is always one if it is the leading digit of a multiplier when the leading digit of a short product is the same as the multiplier digit (Example 7).  It is always 1 as a multiplier digit when its partial product is the same as the multiplier (Example 8).   When the trailing digits of each partial product match their multiplier digits, A is usually 1, but it could also be 6 if all the multiplier digits are even (Example 9; see D-39 and M-40).     The leading digit of the sum of two addends which is longer than either addend is always 1 (Example 10).   When you have identified the value of 1, you can often make other deductions about consecutive digits (more in Section 3).

      B  C            B  C
   V xx xx         V xx xx
     xx              xx
     Ax xx            x xx
     Ax xx            x xx
      x xx            A xx

Leading carries
                                        ....        ....
     F...      F...       A....         ....        ....         ....
 +  BE...  + DBE...    +  B....      + B....      + ....      + a....
    C....    DC....      C.....        C....       C....        B....
       Example 16      Example 17   Example 18   Example 19   Example 20

When the leading digit of an addend which is longer than the others is increased by a carry from the column to its right, we call this a leading carry.  In Example 16 above, we know that [BC]; this is true even if there is a non-carrying digit further to the left.  Example 17 is another sort of leading carry: in this case we know that C = 1.   In additions with more than two addends, we can also have leading carries, but the increase can be larger than 1 (and as large as one less than the number of addends).  In example 18, we can have either [BC] or [B.C]; in example 19, C =1 or C = 2.    In a two-digit sum which carries, neither addend can be zero; in Examples 16, E is not zero (of course the leading digit F cannot be zero either).    Example 19 is a double key problem (see Section 9 in Part 2): a and B are in different alphabets, so either a = B, or [aB] as usual (see K- and M-700 problems).

Nine

   ..A..     ..A..       ..B..          DA...           D..E..       D...E             ....   
 + ..B..   - ..B..     + ..B..        +  B...         +  ..B..     +  ...B         + CA....   
   ..A..       A         ..B..          EA...           E..D..       E...D           DB....   
       B = 0,9         B = 0,9          B = 9          B = 8,9       B = 9       A = 9, B = 0, [CD]
     Example 21        Example 22     Example 23      Example 24    Example 25       Example 26

The situation in Example 21, which occurs frequently in both additions and subtractions, indicates either B = 0 or B = 9.   The same is true of the sum in Example 22 where all three letters are the same; if this occurs in the trailing column, then B = 0; otherwise B = 0 or B = 9 (see A-74 for an easy example).   If the zero case can be ruled out, for any of the reasons we have looked at earlier, including the value of 0 already being assigned to another letter, we can definitely conclude that B = 9.    Example 23, where we can see that there is a carry from A + B = A, immediately shows that B = 9.   In Example 24, we can see [DE], from the leading carry.  Knowing that, the addition E + B = D is possible only if B = 8 (with a carry from the column to its right) or B = 9 (with no carry).   If we know that there is no carry (as in Example 25, where the addition is in the trailing column), we can be sure that B = 9.    Example 26 shows a double leading carry: the third column from the left carries to A, which in turn carries to C.   Since there is a carry increasing A to B, but that carries also, we know that A = 9, B = 0, and [CD] (see D-41 for an example).     We also saw earlier that a digit repeated in adjacent columns of an addition cannot be 9 if both columns contain three different letters.

In Section 4, we will see how 9 can sometimes be identified by multiplication clues (and vice versa).    In section 6, we will see a way to get extra information when 9 is a digit in the quotient or multiplier.

3.  Greater Than, Less Than, and Consecutive Digits

A rich source of information in cryptarithms is the relationships between pairs of letters.  In many situations, it is possible to determine which of two letters represents a larger value, and sometimes that two letters represent adjacent values.   We will use the normal mathematical symbols < and > to indicate less than and greater than (of course A < B means the same thing as B > A).   We also use square brackets to designate adjacent digits: [AB] indicates that A and B represent adjacent digits in ascending order (that is, A + 1 = B).   (We do not use [AB] if it is possible that A = 9 and B = 0).

An important rule to remember with greater than and less than is that they are transitive: If A < B and B < C, we know that A < C, and we can write them as a series of connected inequalities A < B < C.    The relationship of consecutive digits is transitive too: [AB] and [BC] can be combined into [ABC].    Inequalities and consecutive digits also combine: if [AB], and A < C, we know that B < C, and we simply write [AB] < C.    Similarly [AB] and D < B gives D < [AB].

Chains of consecutive digits and inequalities can be longer than three digits; in rare cases all ten digits can be placed in order, as in the Fifth of November problem we'll mention later.

We can often build sequences when we know the value of 0, 1, or 9:
(1) If we know that A = 0, the addition A + B = C indicates [BC], with a carry of 1 from the column to its right.
(2) If we know that A = 1, the addition A + B = C tells us that either [BC] or [B.C].   We can determine which if we know the carry.
(3) If we know that A = 9, the addition A + B = C tells us that [CB]; there is no carry from the column to the right, but A + B = C will carry to the column to the left).

    0                   1                        ...A...   A?D          A...   A < D
  ...A...  A < C      ...A...   A > C            ...B...   B?D          B...   B < D
+ ...B...  B < C    + ...B...   B > C          + ...C...   C?D        + C...   C < D
  ...C...             ...C...                    ...D...                D...   D >= 6

  ..A..B...         ...A..B          AA..      AB..     ..AB
+ ..B..A...       + ...B..A       + EBB..   + EBA..   + ..BA
  ..D..C...         ...C..D         ECD..     FCD..       DC
    {CD}              [DC]          [CD]      [DC]      [CD]
   or 9/0       or D = 9, C = 0

When two additions with the same two addends (in the same or different orders) have different results, the two sums either represent adjacent digits, or one is 9 and the other 0.  If either is a trailing digit it is the smaller of the two (except in the 9/0 case).  The carry from both is the same (again except for the 9/0 case).   The carry to the two additions, however, must be different.   In the first example above, one of the additions must have a carry of 0 to it, and the other a carry of 1.  In the second example above, there must be a carry of 1 to A + B = C.    (The separated columns need not occur in the same addition: they may occur in different subtractions, in a division or root problem.)    In the third example above, with repeated columns adjacent, A + B does not carry, so there is no carry to A + B = C and a carry of 1 to A + B = D.   In the fourth example, the reverse is true.   In the fifth example, there is no carry to the units addition B + A = C, so there must be a carry to B + A = D, yielding [CD] (see D-98, for example).

__________________________________________________________________

Topless Division
V-4 (2 words, 9860435127)
            ....
    ....).......       000      011      011
         OAMD          AROA     ARES     AAEF
         AEDMA      + ADMAE  + AIARR  + ALMDO
         ALMDO        ARESO    AAEFD    AEDMA
          AAEFD   
          AIARR  
           ARESO 
           ADMAE  
            AROA    
______________________________________________________

Let's look at a concrete example, V-4.  This is a Topless Division, a puzzle type we'll look at in more detail later.   The dividend, divisor, and quotient are missing.   At the moment we are only interested in reconstructing the three additions shown.  There doesn't seem to be much to go on, but we have three crucial clues.  The first is that OAMD is a short product, and there are three long products beginning with A.  This means that O is at least as large as the first digit of the divisor, which is at least as large as the first digit of the long product (otherwise the multiplier digit would be at least 10).  Since O and A can't be equal, we know that A < O.  [We'll look much more closely at leading digits later.]  The second clue is the addition A + I = A with no carry.   This tells us that I = 0, but far more importantly, that there is no carry from the addition to its immediate right, so R < E and A < E.   We will mark carries as 0 and 1 as we discover them.  We mark 0 above A + I = A.   The third clue is the pair of additions R + A = E and R + M = E.   This tells us that A and M are consecutive values, though we don't know yet which is larger.  We also know that M < E and the second addition doesn't carry either.    The addition A + E = O tells us, since A < O, that E < O, and there is no carry.   Looking at the other two additions which do not carry: A + D = R tells us directly that A < R and D < R; A + L = E tells us that A < E (which we already know) and L < E.   We also have another pair of similar additions, A + L = E and R + A = E (the same as A + R = E).  We know, just as with A and M before, that L and R are adjacent in value, but we don't know which is larger yet (and the carries to the two additions will have to be different). 

So far we have a series of inequalities that looks like {AM}, D < {LR} < E < O.   [Both curly and square brackets should be thought of as unbreakable blocks: anything less than L is also less than R, and vice versa (and the same for greater than).]  The comma shows that both D and {AM} are less than R, but D might be larger or smaller than A and M.]    As an aside, sometimes when you are doing this kind of analysis, you won't get any further than a partial string of inequalities like this, but the range of possible values for each letter is constrained (e.g. 7 <= O, 6 <= E <= 8, etc.), and it might be possible to work out possible values of certain letters using the additions directly.   But we have a lot more information here, so we will forge ahead.

The addition E + D = M gives us crucial information.  Since M < E, we know that M < D (that is, {AM} < D).  So the addition A + M = D tells us that there is no carry to A + L = E.   This means that there has to be a carry to R + A = E, otherwise R = L.   This greatly helps our deductions: first, we know that R + 1 = L, since A + L is equal to A + R + 1 (both equal to E).   So {LR} becomes [RL]: we know which adjacent letter is the smaller one.   Since we have a carry to R + A = E, we also know that there is no carry to R + M = E, and by the same line of reasoning, R + M = E = R + A + 1, so A is less than M and our inequalities now read [AM] < D < [RL] < E < O.   The second new fact is that, since E + R = F carries, we know that F < E and F < R.   We don't know exactly where F falls, only that it is less than E.   But from the addition F + O = A, knowing that A < O, we know that A < F and there is a carry.  F < R and A < F gets us to [AM] < D, F < [RL] < E < O.   We have all but one letter placed (remembering that I = 0).   S + R = D tells us, since D < R, that D < S also, and again there is a carry (all of the carries are determined, as shown below).   Again we don't know exactly where S falls.  The last addition we have to examine is O + A = S.  We actually deduced before that there is no carry; this is confirmed from the fact that A < S (since A < D and D < S), and therefore O < S.   We have almost completely reconstructed the sequence of letters: adding zero, we have I < [AM] < D, F < [RL] < E < O < S.  We know the exact value of every letter, except for D and F.   F + O = A, since A = 1 and O = 8, gives us F = 3 and D = 4.   The full sequence is [IAMFDRLEOS].  Later we'll see how to reconstruct missing elements from the reconstructed partial products (or you can look up V-4 in the Hints section).    More examples of building sequences are D-44, I-10, I-13, M-12, M-14, M-61, R-4, and R-13.   Sometimes partial sequences merely narrow down possibilities to a point where a problem can be attacked by other clues: see D-201.

A sequence can also sometimes allow additional letters to be calculated.  For example, if we have a sequence [ABCD], and a rightmost addition E + B = D, we can tell that E = 2 (E = 1 if the addition is internal and there is a carry).   Similarly, F + D = A would give F = 7 with no carry, F = 6 with a carry (3 backwards is equivalent to 7 forward).

4. Multiplication Principles: Identities and Odd and Even Numbers

Multiplications with repeated digits

 1  2  3  4  5  6  7  8  9
 2  4  6  8 10 12 14 16 18
 3  6  9 12 15 18 21 24 27         ...A
 4  8 12 16 20 24 28 32 36       x    B in bold
 5 10 15 20 25 30 35 40 45         ...B
 6 12 18 24 30 36 42 48 54
 7 14 21 28 35 42 49 56 63
 8 16 24 32 40 48 56 64 72
 9 18 27 36 45 54 63 72 81

One of the most useful rules to memorize involves multiplications where the trailing digits follow the pattern A x B = B.   If you examine the multiplication table above, showing the products of single digits (we omit the cases of multiplying by zero), you will see that this can occur in four cases:
(1) B = 0 [not shown] (this is often obvious, as we saw in the Search for Zero section)
(2) A = 1 (often obvious too, as we have seen before, because a partial product is the same as the multiplicand)
(3) B = 5 and A is an odd number (3, 7, or 9)
(4) A = 6 and B is an even number (2, 4, or 8)

The six usual cases with repeated digits (A x B = B):

A B
3 5
7 5
9 5
6 2
6 4
6 8

When there is more than one identity in the same problem, we can narrow down the possibilities further:
(1) A x B = B and A x C = C give either A = 6 (with B and C both even), or A = 1.
(2) A x B = A and A x C = A give either A = 5 (with B and C both odd), or A = 0.   Frequently we will also have A x D = E, in which case A = 5, E = 0, and D is even.

In the case where both digits being multiplied are the same (this always occurs in square roots, and occasionally in multiplications and divisions), we have the possible cases A x A = A (A = 0, 1, 5, or 6) and A x A = B (A = 2, 3, 4, 7, 8, or 9).   The trailing digit of a square can never equal 2, 3, 7, or 8.

Frequently we have two of the digits of a multiplication identified, and need to calculate the third.  This is trivial if we have the two digits being multiplied and need the product, and if we have an odd digit multiplier and the product; the result is always unique:  e.g. 3 x 6 = A gives A = 8; 7 x A = 4 gives A = 2.   However, if we have the product and an even digit being multiplied, there will be two possible answers, which will be 5-complements, differing by 5: e.g. 4 x A = 8 gives the possible results A = 2 or A = 7.

Odd and Even Numbers

In addition, the sum of two even numbers is even; the sum of two odd numbers is also even, and the sum of an odd and an even is odd.   This helps us mainly in looking at the trailing column of additions (whether in an addition puzzle or as part of a multiplication or division); for example, in a trailing sum A + A = B, B is always even.  We cannot draw conclusions about internal additions unless we can be sure whether there is a carry.  

A sum of the form A + A = B, given the value of A, might have two possible values for B, depending on the carry to A + A= B (B is even if there is no carry, odd if there is).   Given the value of B, there are two possible values of A, which are 5-complements.  The larger value is correct if there is a carry from A + A = B to the next column:

A 0 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9
B 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8

In multiplication, the product of two odd numbers is odd, while the product of two even numbers, or an odd and an even, is even.    Once we have established a letter as representing an even number, any of its multiples must always be even (this is especially helpful in the case where a multiplicand or divisor ends in an even number, for we can also identify the last letter of each partial product as even).   If [AB] and A is odd, then B is even (and vice versa).   Any group of consecutive letters also alternates in odd and even.   5-complement pairs also consist of one odd and one even digit.   If we know that at least one partial product ends in an odd digit, the multiplicand must also be odd (see M-96).  Occasionally we can separate the ten digits into five odd and five even very quickly: see D-25, M-46, M-53, M-54, and M-74 as examples.

Another valuable rule is that when a digit A has two products with the same last digit B (not equal to A) with two different multipliers (A x C = B and A x D = B), both A and B must be even.   The multipliers C and D are 5-complements; one is odd and the other even.  See M-89 for an example.    The exception to this rule is when B = 0, which gives A = 5, with both C and D even.  If we cannot directly see that B = 0, we can still deduce it if there are three different multipliers with the same product: see M-59 as an example.   

Odd digits (except 5) produce a different last digit for each multiplier.   When a digit A (except A = 0) has products with the last digit A for two different multipliers, A must be equal to 5 (e.g. M-90), provided neither multiplier is 1 (don't get tripped up by a problem like M-91).

____________________________________________________________________
       SUIT      M-60      T H U O L Y D S  I A
     x LOUD    (2 words,   2 6 8 3 4x
       AOHY   5967012384)          9 0 5 3x
     STASH                 4 2 8 3 7 0 5 1  6 9
     DDAH                  6 8 8x
   SOYTU                   8 4 8x
   SOLIDITY
_________________________________________________

In the problem above, we can immediately deduce that T is even, since T x U = H and T x O = H (H + H = T would also tell us that T is even, but the general rule we mentioned above applies more often). The letters U and O are 5-complements.   We also know that H is even, and in this particular problem, we have the added clue that H + H = T.   We can make a small table of the four possible values of T and H.   In each case, the possible values for O and U are 3 and 8 in some order; two of the possibilities are immediately eliminated because 8 is repeated.   We can see that SUIT x O = DDAH is a short product and SUIT x U = STASH is a long product, so we know that O < U, and we can fill in the values of U and O from this fact.   In both cases which remain, O = 3 and U = 8.   We next compute the value of L from T x L = U.   Let's look at the addition S + D + Y + (carry) = L closely: we have already assigned the values 2 (to T or H) and 3 (to O).  S and D are leading digits, so neither is 0.   Therefore Y = 0, otherwise the smallest possible sum of S + D + Y = 1 + 4 + 5, which would carry.   The smallest possible sum is now 0 + 1 + 4 = 5, so the case L = 4 is impossible.   Y = 0 gives D = 5.    Since we have D, Y, and L, we can compute possible values for S from the sum S + D + Y + (carry) = L, knowing that the carry from T + D + T + (carry) must be 1 (even if T = 2, A is not zero and there would in turn be a carry from A + A + A + U = D).    S duplicates in the first case, so we now have only one set of values.   We can compute I from O + S + H + (carry) = I, and A from A + A + A + U + (carry?) = D.

Other multiplication facts

Let's see how to use this technique to solve M-5.  We see from the leading end of the addition that [ND].  For each value of N and D, we can list from the table possible values of O, and for each possible value of O, we can list possible values of R ([ND] = 78 is eliminated since O = 9 and R = 8, duplicating D; [ND] = 67 with O = 8 is eliminated since R=67 duplicates either N or D).  Since R + D is at least 9 (and at least 10 if R > N, since there is then no carry to R + D = A), we can eliminate many possible values of O and R (values of O thus eliminated are underlined in the worksheet table below).   We can also eliminate D = 5 since E x O = D (5 can never be the result of a multiplication involving three unlike digits), and also odd values of D with even values of O (eliminated values in italics).  We are left with only eight sets of values for the four letters NDOR.    We then calculate possible values of E (from O x E = D), eliminating three more cases, and K (from D x E = K), eliminating three more.    We are down to two cases, and we can compute G from the addition G + K = E and M from M + G + (carry?) = N.   This reduces us to one possible case, and we can finish the addition to get the value of A, and check that the remaining value of C is zero by multiplying out.
                                                                             

Table 1: Leading Digits in Decimal Multiplication
                  Single Leading Digit A
Digit   Short Products             Long Products
  B       1    2  3  4         1  2  3  4  5  6  7  8  9
  2      23   45 67 89        -- -- -- --  1  1  1  1  1
  3     345  678  9 --        -- --  1  1  1 12  2  2  2
  4    4567   89 -- --        --  1  1  1  2  2 23  3  3
  5   56789   -- -- --        --  1  1  2  2  3  3  4  4
  6    6789   -- -- --         1  1 12  2  3 34  4 45  5
  7     789   -- -- --         1 12  2 23 34  4 45 56  6
  8      89   -- -- --         1 12 23  3  4 45 56 67  7
  9       9   -- -- --         1 12 23 34 45 56 67 78  8

                          D...
          D           x     C. 
 C...)B....              ..... 
      A....             A.... 
       ....             B.....
           C < 9, D < 9                           

Let's see how this works with a rather difficult multiplication, M-82, which has two partial products whose second digits are zero:
______________________________________________________________________________
Worksheet
M-82  (2 words,     H S O R T      F              H S O R T F N  I      A
 0896457213)        0 2 7 6 (1)    (45)           0 2 8 9 1 4 6  357    x35
     SIR              2 8 4 1      5                4 9 6 3 7 2  58     1x
   x  OF              2 8 9 (1)    (45)             6 9 4 2 3 x
    THAN              2 9 8 (1)    (45)             6 9 4 5 8 2  7      1
   SHES               3 8 x                         7 9 3 6 8 4  x
   STEIN              3 9 7 12     36
                      4 9 6 123    x57
                      5 9 x
                      6 9 4 1235   x358
                      7 9 3 12456  xxx78
                      8 9 2x
_______________________________________________________________________________

Obviously H = 0, since T + H + (carry?) = T does not carry.  We also note that A + S = I does not carry, so S < I.   We have two partial products with zero as the second digit.   SIR x F = THAN gives T < S, so S is at least 2.   SIR x O = SHES gives ten possibilities for S and O when H = 0.  There is no carry from A + S = I, so S = 8 is impossible since O = 9 and there is no value available for I where S < I).  Two cases are eliminated by R x O = S (one valid case splits into two cases for R, leaving eight cases for S/O/R).  For each case we look at each possible value of T where T < S, and find possible values for F from SIR x F = THAN (again with H = 0).   [Values of T with more than one possible F are shown in parentheses.]  Many of the cases are impossible (or duplicate values), and we can eliminate all cases where F = 5, since R x F = N.  Calculating N for each remaining case leaves only four combinations for S/O/R/T/F/N.  One of these is eliminated because there is no available I where S < I.   In the three remaining cases, we check the possible values of I and calculate A from A + S = I.  Four I/A combinations are possible, but only one works for IR x F = AN (shown above right in bold).   Multiplying out SIR x O = SHES confirms the value of E.

Internal Zeros and Split Partial Products

  AB0CD        AB    AB        A0BCD       A    BCD        ABC0D       ABC    D
x     E ==>  x  E  x  E      x     E ==> x E  x   E      x     E ==> x   E  x E
 DFGHJK       DFG   HJK       DFGHJK      DF   GHJK       DFGHJK      DFGH   JK           

____________________________________________________________

M-1 Multiplication  (2 words, 7892563104)

      CROWN     CROWNITSDA   N 4 4 9 9 9 9 9 9
   x   WITS     x!?xxxxxxx   W 2 8 2 3 4 6 7 8
     DRCAAT                  I 8 2 8 7 6 4 3 2
    ARATIS                  
   WCDDIW                    R N W C A I T S D N O
  ACANAI                     0 9 3 5 1 7 2 8 4 9 6
  ASSISTANT                  0 9 6 2 1 x
                             0 9 6 4x
                             0 9 6 8x
                             0 9 7 5x
___________________________________________________________________________________

              
When zero can be found in the interior of the multiplicand or divisor, it is possible to split the partial products into two pieces, giving twice as many opportunities for analysis of leading and trailing digits.  The best case is when the second or second-to-last digit is zero, producing direct multiplications of single digits (see the examples above).   This is useful in big multiplications and small divisions.  In puzzle M-1 below, we have the clue that N x W = I and N x I = W, giving the possible values shown horizontally.   A search for zero leaves only O and R as possible.  If O = 0, we have the split product WN x W = NAI.   None of these cases have the correct leading digit for N given the value of W (in fact, the cases with N = 9 are all impossible anyway, since a long product cannot begin in 9).   So we know that R = 0, and that W x C = AC.   We list the possible values for W and C from possible values of W we already listed.   Three lines are eliminated because they have a carry from W + C = S.   Next we see that I x C = WC, and only one case works.  The value of T comes from T x C = AR. From S x C = DR we find that only one S gives a value for D we haven't already used, giving S and D.   N comes from A + S = N, and the only remaining value belongs to O (verified by the leading digit of the split partial product OWN * I = DDIW).    The American Agriculturist puzzle cited in the introductory section is another good example of this solving technique.  See also D-55, M-13, M-49, M-51, M-122, M-131, M-146, M-148, M-152, M-153, and especially M-16 and M-86 (both of which split into six single digit multiplications!) and M-421 (four singles).   

As we noted above, when single digits are multiplied and produce a two-digit long product, the leading digit of the long product cannot be the same as either single digit: A x B = ?? cannot begin with either A or B, as the other would have to be at least 10.   This often allows a candidate for zero to be eliminated by creating an impossible split partial product.   Examples include D-36, D-72, D-202, M-108, M-129, M-433, and M-822.

Some Examples using multiple techniques

M-88

    AIR      Case 1: I = 9               Case 2: I = 0
 x __MY_
   MOTE      I M R H O     T  S          I M R O  T  S  H  A     Y      E
 _TRIO__     9 2 5 8 0xxxx               0 2 3 6  1  7  5  xxxx
  THOSE      9 2 4 7 8     1  9xxxx      0 2 4 8  1  9  6  7     4xxxx
             9 2 3 6 6xxxx               0 3 2 6  1  7  5  4     9      8
 T<M<Y,H,A   9 3 4 8 2     1  3xxxx      0 4 2 8 (1  9  6  3     xxxxx
             9 3 2 6 6xxxx                       (3  1xxxxx
             9 4 3 8 2     1  3xxxx
             9 4 2 7 8    (1  9xxxx      I<T<M<Y,H,A
                          (3  1          T<R,S

             S<T<M<Y,H,A<I           
____________________________________________________________________________

Let's look at an example which is broken into two cases, M-88.  From the multiplication AIR x Y = MOTE, we can see that M < Y and M < A. Since M < Y, the leading digit of AIR x M = TRIO is less than the leading digit of AIR x Y = MOTE; that is, T < M.  We also see from the hundreds columns of the addition, since there is no carry, M < H.  We summarize these facts in the worksheet, underneath the full problem.  We also note for the time being that the possible letters equal to 0 are limited to ISE (H is not possible because it is the sum of a non-carrying addition).  I must obviously equal either 0 or 9, and we can draw additional conclusions in each case. 

If I = 9, there is a carry from T + O = S, and T>S.  This greatly restricts the value of M, since four numbers (YHAI) are larger than M, and M also cannot be 5, since O would either be 5 or 0.  There are two numbers less than M, so M is limited to the values 2, 3, and 4.  Since M + R + 1 = H (with the carry from O + I = O) and H is less than 9, the maximum sum of M + R is 7. We can tabulate the few cases of M and R (R cannot be 1 or 0 from the right-end of the multiplications), and calculate both H and O.  Three of the seven cases are eliminated by duplication, and in the four cases left we can list all possible values for T where T < M, and compute S.  Only one case is left when duplicates are eliminated.  Since neither I nor S equals 0, E must equal 0, and Y is 5, leaving A with the remaining value of 6.  Multiplying 692 (AIR) by 5, however, does not equal the value 4830 (MOTE).  So this case fails, and we know that I = 0.

Since I is now known to be 0, we have additional clues (see Internal Zeros later under Leading Digit Analysis) from the multiplications R x Y = TE and M x R = O.  Now we also know that T < R, and since T + O = S does not carry, T < S.   This limits T to values 1, 2, and 3.  We also know that M x R has a single digit product, with neither being 1.  This gives us the same possible values as the leading digits of a short product, except that there is no carry, so we know the exact value of O.  Again we look at each possible value of T (always 1 except when M = 4), and compute S from T + O = S (eliminating the case where there is a carry, since I = 0), and H from M + R = H.  There are four possibilities left.  Since we have an internal zero, we now use the multiplication A x M = TR to find the value of A (leaving three cases).  We find the value of Y in the same way from A x Y = MO, leaving one case, and R x Y = TE gives us the value of E and finishes the solution.
                                     
_______________________________________________________________________________________________

_______________________________________________________________________________________________

Multiplying Out

_______________________________________________________________________________________

D-40 (2 words, 6452970318)
         N        N M W  T   c1 O  c2 E P A R L
 MEOW)TRAP        2 1 3  6y 
      WONT        3 1 4  8y
      MALE        4 1 6  x
                  4 1 7  8  [2] 3 [1] 3x
                  6 1 7  2y
                  2 3 6  x
                  2 3 7  4y
                  2 4 x
                  3 2 6  8  [1] 4 [1] 1 9 0 5 7
                  3 2 7  1y
                  4 2 x
_______________________________________________________________________________________


Some puzzles are solved by building the values in the multiplicand and partial products one column at a time.   Let's see how this works with a small division problem, D-40.  There is only one digit in the quotient, but the partial product is a short product, which restricts the possible values of N, M, and W.    We have to consider cases where M = 1, as well as the usual four cases where M = 2 or N = 2.  Since we have the addition M + W  = T, we know that W <= 8, otherwise it would carry.   In fact, since W < T and T cannot be 9 (N x W = T, so T is neither 5 nor 9), we have W <= 7, and N < W, so N <= 6 (this eliminates the two cases where M = 4 or N = 4).    We can disregard N = 5, since N x W = T and T cannot be zero because of E + T = P.    For the same reason, we can disregard W = 5.   This leaves only nine combinations of N/M/W: for each, we calculate N x W = T (cases where T = 0 are eliminated too), and check to see if the value for T is also possible for M + W = T.  We mark an x for values of T which would duplicate an existing value, leaving seven cases to check.  Five of those (marked y) are not possible sums of M + W = T.   With two cases left, we will calculate O from (N x O) + (carry) = N.   We put the carry from N x W = T in a separate column, marked c1, in brackets to avoid confusion with the regular digits (the carries are invisible, and it does not matter if their values duplicate values for the letters).   In the first case, (4 x O) + c1 = 4.  This becomes 4 x O = 2, which gives O = 3 or O = 8 (the latter is duplicated).   In the second case, the carry c1 is 1, so (3 x O) + 1 = 3, or 3 x O = 2, so O = 4.   In the same way, we put the carry from the (N x O) + c1 = N calculation in another column as c2, and then calculate E from  (N x E) + c2 = O.   The first case duplicates the value of O, but the second case works.    We can verify that this multiplication does not carry, and N x M = W.    We then calculate the value of P from E + T = P.   Since the remainder MALE must be less than MEOW, we have A < E and A = 0, giving [OR] and R = 5.  L + N + (carry?) = A gives L = 7.    D-55, D-68, M-44, M-91, M-94, M-132, and M-144 are relatively easy examples of the same technique; M-462 (duodecimal) and M-561 (pentadecimal) are harder ones.

Sometimes the reverse process is effective: see M-3, M-110, M-112, and M-118 for examples where a full partial product is deduced, then divided by its multiplier digit to obtain the whole multiplicand.  (It is usually easiest to use the partial product with the smallest multiplier digit.)

6. Extra Additions: the Hubbuber Trick

In his excellent booklet Solving Cryptarithms, Jack Winter (Crotalus) points out a useful trick discovered by ACA member Hubbuber (George D. Atkinson).  Crotalus originally published this in a brief article on page 127 of The Cryptogram in November-December 1973, describing Hubbuber's observation on his own multiplication C-9 in the July-August 1972 issue.  When two letters occur as digits of the multiplier (in a multiplication) or the quotient (in a division), and you can see that one letter is greater than the other by 1, you can set up an addition involving the two partial products and the multiplicand (or divisor). Specifically, if [AB], with multiplicand or divisor C, then the partial product A x C, plus the divisor C, equals the partial product B x C.   Usually this relationship is seen in the leading carry of an addition, where a carry converts one letter into another.  (M-6, M-14, M-47, M-56, and M-111 are easy examples of this; M-102 a harder one where the relationship shows up later.)  

Let's see a more subtle example, however. In the division below, R + S = E (trailing end of last subtraction). Also, R + S = A (tens column of first subtraction). The latter must include a carry, thus we know that [EA], and we can set up the extra addition shown.  Now we can see that U + R = S (with no carry to the left) and thus U + U = S also does not carry to the left.  One of the two has a carry from the right, so {UR}.  We construct a table of possible values for U, S, and R (eliminating the case where R = 0).  We also eliminate R = 1, since the remainder is less than the divisor, and T cannot be a leading zero.  We add values for E from R + S = E, eliminating those where it carries (it is also found in the second column of the first addition), and value for A from [EA], and values for P from S + P = U.   Only one set of values (shown in boldface) also fulfills E x P = S (A x P = U also checks).  It is a simple matter to fill in the remaining letters; the extra addition saves unnecessary multiplication to verify K.   Problems M-58, M-104, and M-143 can be solved using related tricks.  If you don't see how, check the Hints section in Appendix 3.   This is a highly useful technique which shows up more often than you would think.   It can even sometimes be used late in a multiplication solution, to allow recovery of the last few digits without having to multiply out an entire multiplicand or calculate results from additions with three or more addends.   M-177 was designed to show a cascading series of Hubbuber additions.

__________________________________________________________________________
D-6 Division (2 words, 1-0)

            AE        RURUPS       U S R  E A P T L Y K
 RAKLP)RESTATE      +  RAKLP       1 2 0x
       RSTLRU         RSTLRU       1 3 2  5 6 8
        RLPSEE                     2 4 1x
        RURUPS                     2 5 3  8 9 7
         TYUTR                     3 6 2  8 9 7 1 4 5 0
                                   3 7 4  x
                                   4 8 3  x
                                   4 9 5  x

__________________________________________________________________________

Multiplying by Nine or Five or Two

If we have 9 as one of the digits of the multiplier or quotient, we can make another hidden addition, by the fact that (9 x A) + A = (10 x A).   This doesn't actually provide new information, it just makes it easier to calculate individual digits, since addition is easier than multiplication.   Let's look at a concrete example, D-102:

______________________________________________________________________________________
D-102 Division (2 words, 8705612493)

            N    ABOEAD   N A R T D   B E S V O
 AVERT)ADVERB  +  AVERT   9 4 1 6 4x
       ABOEAD    AVERT0       2 7 3   1 6 8 5 0
        RANTS                 3 8 2x
______________________________________________________________________________________

The addition N + E + (carry) = E gives N = 0 or N = 9; clearly N = 9 since it is the multiplier digit.   So we can create an extra addition, where AVERT x 9 = ABOEAD, and we add AVERT to ABOEAD to give us AVERT x 10, which is AVERT0 (adding a zero onto a number multiplies it by 10; we boldface it here to avoid confusion with O).   This gives us reversed additions T + A + (carry) = R in the main problem and A + R + (carry) = T in the extra addition.   We know that there is a carry to the second addition, since D + T = 0, so we know that A = 4 (there must be a carry to T + A = R also, which we could work out anyway because R + B = D does not carry, and B < D, so S + D = B carries to T + A = R).   We also know that R and T are 5-complements.  In the main addition,  T + A = R must carry to N + E = E (since N = 9), so R < A, which leaves only three possible R/T pairs.  T + D = 10 (we actually knew this anyway, since N x T = D), so we add values of D, eliminating one case by duplication.   Since A + R = T (in the extra addition) does not carry, E + E = R gives even R, and the problem reduces to one case, fixing R/T/D (boldface line).   R + B + (carry) = D gives B = 0 or B = 1, but B cannot be zero because S + D = B would cause S to duplicate T, so B = 1, and E + E = R now gives E = 6.   S + D = B gives S = 8; B + A + (carry?) = V gives V = 5, and A + O + (carry) = V confirms O = 0.

If one of the digits is 5, we can make another hidden addition from (5 x A) + (5 x A) = (10 x A): if for example ABCDE x 5 = FGHIJ, FGHIJ + FGHIJ = ABCDE0 (see D-106 for an example).   This comes up less often because 9 is easier to identify than 5.    If one of the digits is 2, we also have an addition like ABCDE + ABCDE = FGHIJ (see D-205).   Similar hidden additions are available in other bases whenever a multipler digit is one less than the base (see D-283) or half the base in even bases (see D-263).

7. Double and Triple Table Matching

Sometimes it is possible, particularly in additions, to make a table of possibilities for several letters, but then you find that it is difficult to add any further letters.  But you might be able to start an independent table for several other letters, then combine the tables by eliminating duplicates.  Let's see how this works with problem A-25.  There are two similar additions, H + H = E and H + H = M.   Obviously there is a carry to the latter, and H + H + 1 = M (so [EM]).  H + H = M does not carry, so neither does, and we can make a short table of possibilities for H/E/M.   None of these letters is part of any other additions, so let's start a new table instead.  T + T = S, and S is even, since there is no carry from H + H = E.   T + T = S does not carry, otherwise we would have R + R + 1 = S, impossible with S even.  So we make a table of possibilities for T, S, and R, noting that R will be the 5-complement of T.   We do not know yet whether there is a carry to or from G + G = T, but we will list the two possible values (5-complements again) for G in each case.   Now we combine the two tables, eliminating every case with duplicates (e.g., HEM = 123 duplicates at least one digit with every TSR combination except 489, and G must be 7 to avoid duplicating 2).  For each of the five unduplicated sets we note the three missing digits.   The remaining three letters OAI are interrelated, so we make a third table.  There must be a carry from O + O = A to H + H = M, so O must be at least 5.  We also know that there is a carry to A + A = I (since R is always at least 5), so in each case we list both values for A (carry from G + G = T or not) and the corresponding values for I, and look for a corresponding triplet in the OAI table.  Only one combination matches (marked with ***), and the problem is solved.    See M-147 for another example, where two tables combine early and eliminate many cases from each.     Also see R-60, solved as an addition.    A-2 is similar to A-25, using three tables containing all ten digits.   R-30 is a difficult base 13 example using two tables, which reduce to a small number of combinations.

______________________________________________________________________________________________________

A-25 Addition (2 words, 8359417026)

    1??100        HEM      TSR G      HEMTSRG  missing       O  A   I
    HOGARTH       123      126 0,5    1234897   056          5 0,1 1,3  ***
 + _HOGARTH_      245      247 1,6    2453681   079          6 2,3 5,7
    MATISSE       367      368 1      3674892   015  ***     7 4,5 9,1
                  489      489 2,7    4891260   357          8 6,7 3,5
                                      4891265   037          9 8   7

______________________________________________________________________________________________________

8. Interlocking Equations

These problems usually consist of six equations (3 vertical and 3 horizontal) which share a set of nine numbers. There are quite a few combinations of operations possible. In solving, it is usually necessary to jump frequently from one equation to another to find letter values. One important point is that there are no partial products shown for multiplications (and divisions, which are exact: there are no remainders). Clues from the final digits are usually helpful.  It is possible to use leading digit analysis, but you must be careful: when considering a multiplication such as A... x B... = C...., it is important to observe that C might be larger than the normal values on the LDA chart. You should consider as possibilities for C the values which can result from A+1 and B, A and B+1, and even A+1 and B+1.  For example, note that 3xxx and 2, or 2xxx and 3 always produce a short product (one letter/digit shorter than the sum of the lengths of the multipliers), but that 3xxx and 2xxx might produce a long product; e.g. 28 x 38 = 1064).   Problems of this type appeared regularly in Cryptography (as Cryptequations, by Rocky Da Monduelli) and occasionally in Four-Star Puzzler (by Thomas K. Brown).  A few can be found in the book by Degrazia (details in Appendix 1).  Many different patterns of operations are possible, as described later in Construction Techniques.  A few sources call them Arithmogriphs, sometimes generating them with symbols instead of letters.

Here is a sample problem, I-1.  For each possible value of M, get L and S from M x M = S and L - M = M (in other words, M + M = L).   L must be greater than S, since A + S = L in the leftmost column of the addition.   Only three cases for M/S/L are possible after eliminating duplicates.   From L and S, list possible values for A from the division LUDBA / EM = DUSS (which indicates that M x S = A).   We have reduced to one case.   We can get the value of E from the subtraction, which is equivalent to PAM + EM = PSL, so E + A + (carry) = S.   Note the internal additions A + E = D; since M + M = L carries to E + A = S, there can be no carry to A + E = D, so [DS].   The value of U comes from L + E + (no carry) = U.   P cannot be 0 (as a leading digit), so either B = 0 or R = 0 in the addition R + M + (carry) = B.   B = 0 doesn't work (R duplicates 1), so R = 0 and B = 9.   We can check the remaining value for P by checking either of the horizontal divisions.

___________________________________________________________________
I-1 Interlocking Equations (2 words, 0-9)

ALARM / PSL =   SM     M S  L   A    E  D  U  R  B  P
   +      -      x     1 1x
SEEMS / PAM =   UM     2 4  4x
   =      =      =     3 9  6x
LUDBA /  EM = DUSS     4 6  8   4x
                       5 5x
                       6 6x
                       7 9  4x
                       8 4  6   2    1  3  7  0  9  5
                       9 1  8   9x

 _________________________________________________________________________________

A double-key problem is one in which the various numbers are divided into two groups, and each group is encoded using a different keyword, usually one using lower case letters and one using upper case letters. Many issues of The Cryptogram contain one of these, most often divisions.  In the most commonly seen variety, the quotient, divisor, and partial products are in lower case letters using one keyword, and the dividend and partial differences are in upper case letters using a second keyword (or vice versa, which makes no difference).   This problem can be solved in a two-step process.  First solve the lower case letters using multiplication clues (the leading and trailing digits of the partial products should enable us to find many of the digits). Then use the lower case values to solve the upper case letters, using the subtractions.

Let's look at an example, problem K-2. Clearly t is 0 and s is 1. Since w x b = w, w x r = w, and w x w = w, w must be 5. Then b and r are odd and o is even. The leading digit of the long product of o x elbow is w, so o must be larger than w, and we can list possible values for o and e from the LDA table. Now we can get the value of b from the next-to-last digit of o x ow. This eliminates all but one possible value of o and e.  Next, find the value for u by looking at the next-to-last digit of the multiplication ow x w, the value of c from the leading digit of w x elbow, the value of l from the leading digit of b x elbow, and finally the value of r from the values of u and e, using the leading digit of r x elbow = uorebw.

________________________________________________________________________________
K-2 Double-Key Division 2 WORDS, 0-9; 2 words, 9-0    

             brows
  elbow)INTIMIDATE      t s w o e b u c l r   A L D E T I V M N O
        lbsoew          0 1 5 6 8 9 2 4 7 3   1 4 9 5 3 8 6 0 2 7
         TNANTD                 9 9 5 0
         uorebw                 8 6 8
          EOTLLA                7 8
          wullbt
           LEVEAT
           crbeuw
            AVVIIE
             elbow
             OIDNM

Now we find the values of the upper case letters.  Note that the leading carries with mixed cases can have the lower value one less than the upper as usual, but they can also be equal (e.g. w and E can either be w = E or [wE]).  Clearly A is 1. Since c + (carry) = L, L must be 4 or 5. Then L + w = D, so D is 9 or 0. Since L + u = O cannot carry (the largest value of L + u = 7), we know that E = w. Since E = 5, L must be 4 and D is 9. There is a carry from E + o = N, so T must be 3 (one greater than u). From T we get I = 8. From I + u = A we know there is a carry to V + e = E, so we get V + 9 = E, and V is 6. The value of M comes from M + w = E, N from E + o = N (1 is already claimed by A, so N is 2), and finally O from O + e = AV. A short-cut for finding the first few digits, in difficult problems, is to multiply out the known quotient and divisor (or add up the partial products). In this problem, we multiply 93651 x 87965 to get 8238010215. Since 8238010215 + OIDNM = INTIMIDATE, we know the values of I, N, and T at once. M can be either 0 or 1 (obviously 0, since A = 1). 

A more difficult problem exists when the quotient is upper case and the divisor is lower case (or vice versa), as in K-4, K-5, and Z-3, or when the partial products are in one case and the divisor and quotient are in the other (K-6).

Double key problems (most often divisions) are seen frequently in The Cryptogram; for some reason duodecimal problems have historically been more common than decimals or other bases.  There have been a few triple key divisions: JA78 C-Sp (base 11) and ND84 C-Sp-2 (base 10), both by Li'l Gamin; SO83 AC-234 (base 12) by Mordashka.   Li'l Gamin even produced a quadruple key division: JA86 C-Sp-2 (base 11).    Multiplications can also be constructed: the problems starting with M-701 here are double key decimal multiplications (I also had one in The Cryptogram, JF99 C-13); a triple key decimal multiplication can be found as Challenge Problem Z-10 (or you can see this as a bottomless double key).

Another slight variation which eliminates the need for lower case letters is to use twenty different letters (see problems starting with K-21).  These have to be divided into two separate sets, each set assigned to 0-9 as usual.  To prevent the number of combinations from being too large, we specify that each word in the puzzle (whether coherent or not) contains letters from only one set.   This makes separating them easy.

10. Magic Squares

A magic square is an array of numbers with the property that the sum of the numbers in each row, each column, and the two long diagonals, is the same.   In Q-2 below, FF + POP + ERG + PGI = AIR, the same sum as the other three rows and four columns, and the diagonals (e.g. EON + POP + TEA + AI = AIR).   The Bibliography lists several books devoted to magic squares, and Part 4 contains a section on constructing magic square cryptarithms.  The first magic square cryptarithm seems to be from The Sphinx in September 1934 (see the book by Brooke, problem 81, p. 30), a 5x5 keyed square in which the sum is given as 275 (most magic square cryptarithms now encipher the sum as well).

Q-2 Magic Square 2 words, 4029758163

PNF EAR EFT  AI  sum     E P N    A    R   I  O   F    T    G
PPE  TE TEA EPA  AIR     1 2 7   56   x4   9  0   38   83   5
 FF POP ERG PGI          1 3 6   78   xx  
EON PIN  GO PRO          1 4 5    9    0   2  7x
                         2 1 7   56   4x   x
                         2 3 5   89   0x   4  x
                         2 4 4x
                         3 1 6   78   02  x7  0   x
                         3 2 5   89   x4   8  x
                         3 4 4x

_______________________________________________________________________________________

_______________________________________________________________________________________

Q-8 (3 words, 2345907186)

THEG AMES CAFE    sum
ECSC AEGM GFOA    ECTHA
TOTT HTAF HFHO
_______________________________________________________________

The addition CAFE + GFOA + HFHO = ECTHA is the most useful of the eight sums.  To begin with, the thousands column shows C + G + H + (carry) = EC.   Even if G and H are as large as possible (9 and 8 in some order, and the hundreds column carried over 2, it would be impossible for the sum to be larger than C + 19, so E cannot be equal to 2 and must be 1.   From the ones column, E + A + O = A indicates, regardless of the value of A, that E + O = 10 (zero is impossible since at least one must be larger than zero).  This addition carries one into the tens column, so that F + O + H + 1 = H, from which we know that F and O must add up to 9.   Since we know that E is 1, this makes O equal to 9 and F equal to 0:

  2  3  4  5  9  0  7  1  8  6

  _  _  _  _  O  F  _  E  _  _ 

Now we can look at the ones columns of some of the other additions. Since T + F + O = A (bottom row addition), T + 9 = A, and the addition T + M + E  = A (diagonal from TOTT in lower left to CAFE in upper right) indicates that M + E equals 9, so M equals 8.   C + M + A  = A (second row) indicates that C + M = 10, so C equals 2.    Since T + 9 = A, G + C + T = A (left column addition) indicates that G + C = 9, and G equals 7.    Look at the thousands column of that same addition: E + T + T + (carry) = 12.   The carry cannot be larger than 2 (the three numbers added together plus another carry can be at most 8 + 9 + 9 + 2 = 28), so T must be at least 5, and at most 6, since 7, 8, and 9 have been assigned letters already.   From T + 9 = A, we find that A is 4 or 5 respectively, if T is 5 or 6.  From the tens column of the bottom row addition, T + A + H + (carry) = H, so T + A equals 9 or 10 depending on the carry.   A must be 4 and T is 5:

  2  3  4  5  9  0  7  1  8  6

  C  _  A  T  O  F  G  E  M  _ 

H cannot be 6, since the thousands column of the bottom row is T + H + H + (carry) = 12, and H = 6 would make the sum at least 17.  H must equal 3, and S equals 6.    (We can check by adding each row, column, and long diagonal to see that each adds to ECTHA = 12534.)   The complete solution is:

  2  3  4  5 / 9  0 / 7  1  8  6

  C  H  A  T / O  F / G  E  M  S

Two of the Challenge puzzles, Z-7 and Z-8 are unusual: Z-7 is a regular 4x4 magic square, but the sum is not specified; Z-8 is a magic square where the magic constant is the product of the four numbers in each row, column, and main diagonal.

11. Additions With More Than Two Addends

Additions with three or more addends are much more difficult than those with only two addends, because the number of combinations in each column increases with each additional addend, the range of possible carries is larger, and the critical greater-than-less-than principle we saw earlier no longer applies.   Such additions are frequently seen as alphametics.   Of course they also occur as part of multiplications where the multiplier is more than two digits long, but because the partial products are offset, there are often easier clues in the second and next-to-last columns.  One principle to remember is: the largest possible carry in an addition is one less than the number of addends.

    NASAL    A-10 (2 words, 2739015846)
    DUETS
  + LUNGS
    TREAD

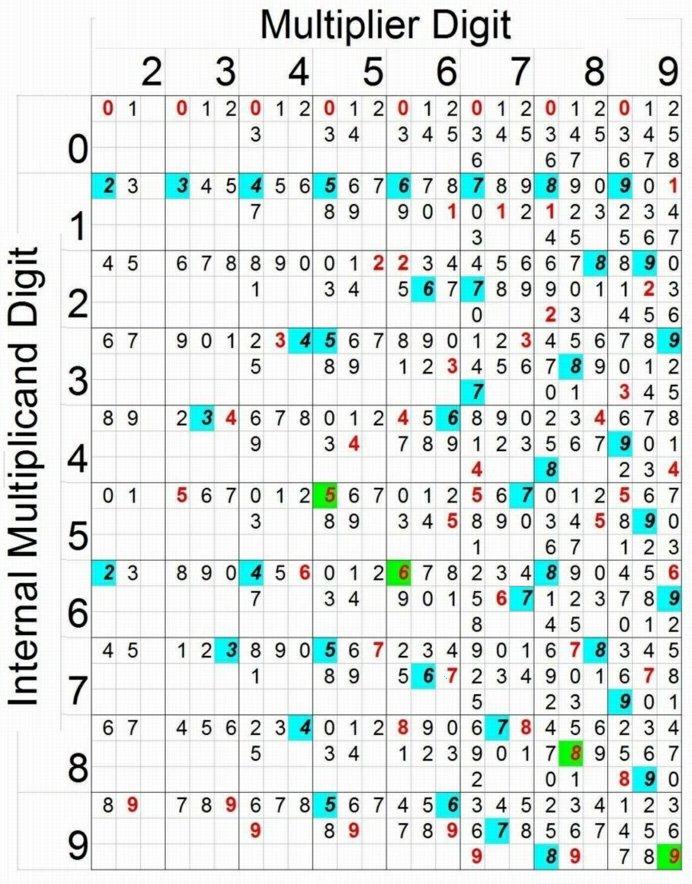
12. Single-Digit Multiplications and Internal Multiplication

Above is a table showing every possible value of an internal multiplication of the form:

    ..A...
 x       B
    ..C...

... highlighting values where one or more of the letters are repeated.  This can be useful in solving certain single-digit multiplications.  

     OVERDUE     M-620  (2 words, 7851304629)
 x         E
    ARSENALS

Above is a fairly easy example, where the possibilities are greatly restricted at the very start.  When the multiplier, internal digit of the multiplicand, and internal digit of the product are identical, there are only four possibilities: 5, 6, 8, and 9 (highlighted in red on green).   9 almost never occurs (see the notes on the table below).   In the example above, the rare conditions for E = 9 do not occur, and we can also see that E cannot equal 5 or 6, since  E x E = S at the far right.   Therefore E = 8, S = 4, and the carry from E x R is 4, so R equals either 5 or 6.  We also see that the carry from E x E is 6, and E x V = (S - 6) = 8, so V = 1 or 6 (of course V and R cannot both equal 6, so we have three cases for E/S/R/V).  Since E x O = (R - carry), we can calculate O, and only in the first case is there a valid value (8 x O cannot equal 9 or 5).  We thus have O = 3, and A = 2.  Now (8 x U) + 6 = L, and we can try the four unused values (0679) for U, to find that only U = 0 and L = 6 works.  There is no carry from E x U = L, so E x D = A, and D = 9.  The carry is 7, and (E x R) + 7 = 7, which is the last unused value, which equals N.

   E S R V  (carry from ExV)  O  A  U     L    
   8 4 5 1         1          3  2  0679  6xxx
   8 4 5 6         6          x
   8 4 6 1         1          x

Values for Triply Repeated Internal Multiplication

    ..AB..
 x       A
    ..A...

The table above shows possible values for an internal multiplcation where the three digits are identical, as well as possible values for the multiplicand digit to the right which could produce the correct carry.    See D-66 for an example of a triple internal repeat.
 A  B    carry
  5  0,1    0
  6  0,1    0
 8  5,6    4
 9  8,9    8*

*If A is 9, the multiplication must be a quadruple repeat ..AA.. x A = ..A.., or else B must be 8 followed by 9, 89, 889, etc. 

Now consider the problem below, inspired by Alice in Wonderland:

    UGLIFI     M-621    (2 words, 0384196752)
 x       G
    CATION

As this is a short product (the product is the same length as the multiplier), the possible values for U, G, and C are severely limited.  Either U is 1, or U is 2 and G is 3 or 4, or U is 3 or 4 and G is 2.   Considering the possible carries from the multiplication of G x G in the second leftmost column also gives us possible values for C.  If G = 2, there is no carry, and U cannot be 1 (since C = G x U, and C= G).  If U = 1, G cannot be larger than 6, otherwise the carry makes C greater than 9.  The possible sets of three values are shown in Table 1 below left, x indicating no possible unrepeated value):

 U G C        G I              G A
 1 2 x        2 09             2 45
 1 3 4        3 0459           3 901
 1 4 5        4 0369           4 6789
 1 5 7        5 024579         5 56789
 1 6 9        6 012345789      6 678901
 1 7 x
 1 8 x        Table 2          Table 3
 1 9 x
 2 3 6
 2 3 7
 2 4 9
 3 2 6
 4 2 8

Table 1


For each value of G, we can extract from the full table at bottom all of the possible values of I (that is, the values where the product equals the internal digit of the multiplier).  These are marked in red on the table (and summarized in Table 2 above center).  Clearly we can omit all values where I = 0 or I = 1, or where I = 5 and G is odd, or where either = 6 and the other is even.  We list the others below, appending the value of N (from I x G = N) for each, and marking x where N repeats a value already assigned.  10 valid cases remain.  For each of these, we consider the carry to G x I = I, and list the unduplicated values of F which will produce the desired carry from F x G (these can be calculated on the fly or extracted from a Leading Digit Analysis table).  For example, on the first line, F x 3 produces a carry of 2 when F is at least 6, so we have unused values of 6 and 8.    On each line, we then multiply out F x G, adding the carry from I x G to the product to obtain the value of O.
             
 U G C I   N  (carry   F  (carry      O
              to GxG)      from IxG)
 1 3 4 9   7     2     68     2       06
 1 4 5 3   2     1     x
       9   6     3     78     3       xx
 1 5 7 2   0     2     4      1       x
       4   0     4     89     2       2x
 1 6 9 3   8     5     x
       5   0     5     8      3       x
       7   2     5     8      4       x
 2 3 6 4   x
       9   7     2     8      2       x
 2 3 7 4   x
       9   x
 2 4 9 3   x
 3 2 6 9   8     1     57     1       15
 4 2 8 9   x

We then remove duplicate values and compress the table to the five valid lines, then add possible values for A (from G x G = A), summarized above in Table 3.  Only four cases remain (one with two values of A).  With eight letters established in each case, we try the remaining values for L and check that L x G plus carry = T.

 U G C I N F O A (carry from GxI)  L     T
 1 3 4 9 7 6 0 x    
 1 3 4 9 7 8 6 0      2            25    xx
 1 5 7 4 0 8 2 69     2            369   xxx
 3 2 6 9 8 5 1 4      1            07    xx
 3 2 6 9 8 7 5 4      1            01    1x

The correct values are on the last line, where L = 0 and T = 1, and the problem is solved.

Special cases

    ...1...
 x        A 
    ...B...

When the multiplicand contains an internal 1, the internal multiplication above always has a carry of 0 when A <= B (which is always the case when A <= 5), and a carry of 1 when B < A.   See M-15 for an example.

    ..BA...      A   2     3     6     7     8  
 x        A      B  1,6   1,4   2,7   6,9   4,9 
    ..AC...                                     

Puzzle D-34 can also be solved quickly using a different clue from internal multiplication (see Hints).   D-19 and M-203 also use part of the general table.

13. Topless Divisions and Related Puzzles

In Games Magazine ("Rent Calculation", Wild Cards, February-March 1989, page 52), Henry Hook posed a curious cryptarithm: a division in which the top two lines (showing the dividend, divisor, and quotient) are omitted. The solver is forced to rely on addition clues only to find the digit corresponding to each letter, then reconstruct the dividend, divisor, and quotient from the partial products.  Similar problems by Eric Emmet appeared earlier in New Scientist (see Bibliography).  I introduced this puzzle to The American Cryptogram Association in 1998 as Topless Divisions (The Cryptogram, C-Sp-1's in July-August and September-October 1998, July-August 1999, and May-June 2000).   Usually some or all of the missing words are coherent.  Let's see how to solve one of these.  Here is V-1; we have filled in the digits of the divisor which we can see dropped down into the subtractions:  

_______________________________________________________________________________
V-1  (2 words, 5849136072)

    ...)...SKIN  
        PRO         RIESNKOA PL           SOI       PRO    607
        SOIS        08912473 65         + PRO       SNSK  1214
        SNSK           23563x             OIL       LKPA  5463
         LPOK          34653x                       SINS  1821
         LKPA                                       NKNI  2428
          NSSI 
          SINS 
           NEON
           NKNI 
            LKK
______________________________________________________________________________

A search for zero shows us that R is the only possibility, which doesn't help us much, but we'll mark it anyway.  We can see that [SN] from the leading carry of the fourth subtraction, and we also have E + N = S, so E is either 8 (if O + S = I carries), or 9 (if not). P is larger than either N or S (LPOK - LKPA = NSS), but S + P does not carry to the hidden quotient, so S is at most 3 (otherwise S is at least 4, and P is at least 6).  Since E is greater than S, E + N = S must carry, and N + I + 1 = S, so I is 8 and E is 9.  Now we can simply list the possible values for S and N, and compute K, A, and O for each, using the rightmost ends of the last three subtractions.  Two of these produce duplicate values and can be eliminated, and we can calculate the two remaining values (P and L) and recover the keywords.  But part of the puzzle is also to reconstruct the rest of the division.

Once the letter equivalents have been determined, the dividend can be recovered by addition, reversing the first subtraction (we can see that the dividend in our example is OILSKIN). To determine the divisor and quotient, divide the largest partial product by the smallest. The ratio will usually indicate what digit of the quotient corresponds to each partial product. For example, if the ratio is 4.5, the largest partial product is 9 times the divisor and the smallest is 2 times the divisor.  When the divisor has been found, the quotient can be computed, often by sight, one digit at a time.  In our example, 5463/607 is 9, so PRO = 607 is the divisor, and the quotient is 12934 = SNEAK.    In harder problems there might be more than one possible solution to the additions, and each case must be tested separately to see which one produces valid partial products with integer quotients (see Enigma 209 cited above, or V-9 herein).    Sometimes it is easier, when two partial products start with the same letter, to subtract the smaller from the larger, to see if the difference makes a divisor which divides each partial product evenly.  This method works here too, as SINS - SNSK gives the correct divisor 607 too.

It is also possible to construct a Topless Multiplication or Root along the same principle.  Crotalus constructed a Topless Square Root (even missing its first partial power) which appeared as C-Sp-1 in The Cryptogram in November-December 2000.   Problem R-36 herein is a Topless Cube Root; R-50 is a Topless Fifth Root (the single addition has a unique solution: the first letter of the root is given because it would be tedious to find the first power otherwise).   Eric Emmett published a few multiplications missing only the multiplicand, in New Scientist (see Bibliography).   M-801 herein is a (very hard) ideal multiplication with both multiplicand and multiplier missing: the addition has two (similar) solutions and each case must be tested as mentioned above.   Z-17 is a Topless Multiplication with the last digit of the multiplier specified; without it the problem would be even more difficult.   If the multiplier digits have common factors, it is necessary to add at least one letter of either the multiplicand or the multiplier to give a unique solution (for example, M-804 could have two different multiplicands without a letter being specified).

A different idea is a Bottomless Multiplication (a fairly easy example of mine appeared in The Cryptogram, C-Sp-1, September-October 1999): here the solver must use multiplication clues from the partial products only, to recover all the letter equivalents, before adding or multiplying to discover the product.   [A keyed duodecimal example was published by accident in The Duodecimal Bulletin in September 1946 (Vol. 2, Num. 2, p. 19) in Mary Lloyd's Mathematical Recreations column.]   Solving these usually involves slowly building up the partial products by multiplying out from either end (LDA will be very helpful in most cases).    Some might use the techniques just covered in section 12, especially small ones like Z-15.  Here's another example:

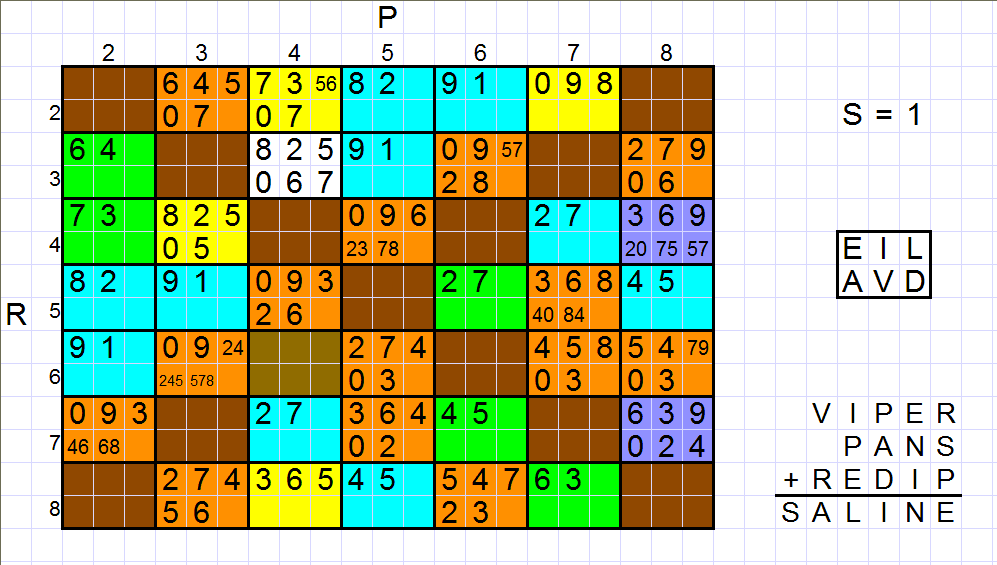
The principal fact we can observe is that S = 1 due to the leading carry (V + R + (carry) cannot exceed 9 + 8 + 2 = 19).  We also see that E + I = 9 or E + I = 10, depending on the carry from the trailing column (the carry cannot be 2 since S = 1, giving a maximum of 1 + 8 + 9).   A search for zero turns up too many candidates to be useful (and knowing zero doesn't help much in three-addend puzzles anyway).   R and P are leading digits and cannot be zero.   Since S = 1, we can see that neither R nor P can be 9 (e.g. if R = 9, 10 + P = E, which is impossible).   So we construct a large table of all the values of R and P from 2 to 8, filling in the rectangles where R = P.   This leaves 36 cases (these could be listed in a regular table, but this is more compact).   In each rectangle, we calculate E from R + S + P = E, placing the values in the upper left corner, and I (upper middle) from E + N + I + (carry) = N (i.e. E + N + (carry) = 10).  The rectangles shaded in light blue (10 cases) are eliminated by duplicating the value of R, S, or P, and we ignore them as we proceed forward.  

Part 3: Other Bases

Our ordinary arithmetic is in base 10, where each column represents 10 times the value of the column to its right.  Arithmetic can be done in any base; base 12 has been promoted as a more desirable alternative because 12 has more divisors than 10. Cryptarithms in other bases have been published: The Cryptogram frequently includes duodecimal (base 12) and undecimal (base 11), but much less frequently other bases.   The only base 14 problem from The Cryptogram I show in my notes is a division by Zer-O, C-Sp in May-June 1980.   Base 14 (tetradecimal) is actually very similar to base 10, as it is twice a prime: 7 and 8 in base 14 have properties similar to 5 and 6 in base 10.  GGMA published a cube root and a fourth root in base 15 in his article in November-December 2007 (see the Bibliography).   I have had a pentadecimal multiplication as C-Sp-2 in September-October 2022 and a hexadecimal division as C-Sp-1 in May-June 1991.  The September-October 2011 issue included, in the Analyst Corner (AC-992), a set of four separate additions in base 17, by Apex Dx; he did a later puzzle in base 19 with mixed addition and multiplication (January-February 2013 AC-1035).  

For many years The Cryptogram used X and E to represent 10 and 11; nowadays A and B are used, for consistency with hexadecimal notation, and we will do the same here.  To avoid possible confusion with letters in the puzzles, I will follow a suggestion by Bill in The Cryptogram, and use lower case letters for the extra digits in bases larger than 10 (sometimes boldfaced in the text).   I will also use X, Y, and Z as variables instead of A, B, and C.

Multiplication in other bases

The principles described earlier for odd and even numbers apply only to even bases.  In odd bases such as 11 or 13, it is not even possible to determine whether a number is odd or even from its last digit: e.g., in base 11, 17 is even but 27 is odd.  In odd bases, the single-digit addition rule for odd and even numbers holds unless there is a carry: when there is a carry of 1, the usual parity of the sum is flipped.  Adding odd to odd, or even to even, produces an odd sum when there is a carry (e.g. in base 11, 5 + 9 = 13 and 8 + 4 =  11), while adding odd to even produces an even sum (8 + 9 = 16).   In additions with multiple addends, the parity is normal if the carry is even (e.g. 0 or 2), but flips if the carry is odd (e.g. 1 or 3).   For example, 5 + 6 + 7 + 8 = 24 in base 11 (remaining even with a carry of 2, as it would in base 10), but 4 + 5 + 6 + 7 + 8 + 9 = 36 (flipping from odd to even because of the carry of 3).

Multiplications of trailing digits follow the same rule: an odd carry flips the usual parity of the trailing digit of the product, while an even carry does not (in base 13, 7 x 6 = 33, but 7 x 8 = 44).

The square of a non-zero digit can only be zero in bases with multiple factors of the same prime: e.g. 4, 8, 9, 12, 16, 18, 20...  

If X x Y = Z in a prime base (2, 3, 5, 7, 11, 13, etc.), Z cannot be zero unless X or Y is zero.   There are other possibilities in composite bases such as base 9, 12, etc.

The multiplicative properties of the digit 5 in base 10 are transferred in other even bases to half of the base: e.g. 6 behaves in base 12 multiplication just as 5 does in base 10, producing 6 as a product with odd multipliers and 0 with even ones.  

Even bases which are twice an odd prime have corresponding digit pairs, e.g. base 14 has 7-complements.  The identity multiplication X x Y = Y has a similar set of solutions to those in base 10: e.g. in base 14, either X = 1; Y = 7 and X is odd; or X = 8 and Y is even.

The reciprocal multiplication pairs X x Y = Z and X x Z = Y hold true in any base when X is one less than the base: Y + Z adds to the base in each pair. See the example in base 11 below: a is one less than the base, and a x 2 = 9 and a x 9 = 2, etc., 9 and 2 adding to eleven.    Composite bases might have additional solutions (4 x 2 = 8 and 4 x 8 = 2 in base 10): see Table 2 in Appendix 4.

   1  2  3  4  5  6  7  8  9  a
   2  4  6  8  a 11 13 15 17 19
   3  6  9 11 14 17 1a 22 25 28
   4  8 11 15 19 22 26 2a 33 37
   5  a 14 19 23 28 32 37 41 46
   6 11 17 22 28 33 39 44 4a 55
   7 13 1a 26 32 39 45 51 58 64
   8 15 22 2a 37 44 51 59 66 73
   9 17 25 33 41 4a 58 66 74 82
   a 19 28 37 46 55 64 73 82 91
    Multiplication table for base 11

            Short Products                Long Products
Digit      1   2   3   4  5      1  2  3  4  5  6  7  8  9  a
  2       23  45  67  89  a     -- -- -- --  1  1  1  1  1  1
  3      345 678  9a  -- --     -- --  1  1  1  1 12  2  2  2
  4     4567 89a  --  -- --     --  1  1  1 12  2  2 23  3  3
  5    56789   a  --  -- --     --  1  1 12  2 23  3 34  4  4
  6    6789a  --  --  -- --      1  1 12  2 23  3 34  4 45  5
  7     789a  --  --  -- --      1  1 12 23  3 34 45  5 56  6
  8      89a  --  --  -- --      1 12  2 23 34 45  5 56 67  7
  9       9a  --  --  -- --      1 12 23 34  4 45 56 67 78  8
  a        a  --  --  -- --      1 12 23 34 45 56 67 78 89  9
       Table of leading digits for base 11 multiplication

________________________________________________________________________

Undecimal  M-431 (2 words, 154a3782960)

      WAVE
    x  TWO       ECORN    W E R O N L T V A C S
     ECORN     +  WAVE    6 3 7 5 4 2 8 a 9 1 0
    ETNWR        ETNWR
   OSLOL 
   ONESEEN

Z-4 Tridecimal Multiplication         
(2 words, 8ca19342b0657) 

Part 4: Construction Techniques

Once you have experience in solving cryptarithms, you might want to try your hand at constructing them. There are numerous methods of construction; I will outline the methods I have used in producing the problems in this magazine.  In virtually all of the problems in this issue, the letters spell out a word or phrase, either in a standard order such as 1-0, or in a mixed order specified with the problem.  The difficulty level in composing cryptarithms depends more on the extent to which the problem is coherent, than the operation involved. 

Many of the problems in this issue were produced by framing a computation, searching for words which would fit a multi-digit number.   By framing I mean the process of converting the digits of an already formulated arithmetic problem into letters, trying to use words for as many of the number elements as possible.   Some of the computations were carefully constructed by hand to illustrate particular techniques.  Others were randomly generated as incoherent problems with the letters ABCDEFGHIJ; I then solved each problem, looking for problems with a variety of difficulty levels (discarding most of those that were trivial or too tedious to solve by hand).   I then attempted to frame the problems I liked.  Sometimes with small problems I was able to include several actual words and still produce coherent keywords in one of the standard orders; in other cases I made a keyword using a mixed order of digits (this is not permitted in The Cryptogram).   Many of the puzzles I created with standard order keywords I submitted to The Cryptogram rather than using them here.  A pattern word dictionary or cryptogram solving program can be helpful in finding words to match sequences of digits.

Certainly the easiest method for the beginning constructor to create a nice problem is to use keywords. Start with a phrase of two or more words totalling ten letters, with no repeats.  [I almost always avoid a single 10-letter keyword, to make solution by anagramming harder.]  Assign the letters to digits in one of the four common orders 0123456789, 1234567890, 9876543210, or 0987654321.   Select the type of problem you want to construct (addition, multiplication, division, square root, etc.), and select two words (one if a square root) which can be made from your ten letters.   Substitute the appropriate digits and carry out the calculation using the resulting two numbers as addends, multiplicands, dividend and divisor, etc.  The lengths of the words should depend on the type of problem and how difficult you want to make it.  Check that all ten digits appear in the calculation, substitute letters for digits, and solve the problem to test it.  Generally the answer and other numbers in the problem will not make sensible words. In making division cryptarithms, however, it is often desirable to have the quotient be a word also. This requires that you keep trying different divisor words until you find one which produces a quotient which also makes a word.  It might also help to try all four standard keyword orders. Another way of going about creating a division with three words is to choose pairs of words as divisor and quotient (if they are of different lengths, the longer should be the divisor, and the shorter the quotient). Multiply the resulting numbers together to see if the first few digits of their product form the start of a usable word. If so, use that word as the dividend, and divide to see that the remainder (which will not form a sensible word except by blind luck) is smaller than the divisor. It might take dozens of tries to find a pair of words that produces a usable dividend: great patience is required here.   In most newsstand puzzle magazines (such as Dell and Official) it is a requirement that division cryptarithms (Dell calls them Word Arithmetic) have a coherent dividend, divisor, and quotient, and there is also a fixed keyword order of 0123456789.

What makes a good problem?   This is a matter of taste, and depends on how difficult you want the problem to be.  Obviously the arithmetic needs to be correct, and contain no leading zeros.  Almost without exception, it should be ideal: that is, it should be complete (containing every digit) and have a unique solution.  If it has a mixed keyword (or no keyword in a Cryptogram problem), it should have a high degree of coherence: all of the words in an addition, or as many as possible in other types, should be coherent.   Keywords which are thematically connected to some of the words in the puzzle are an especially nice feature: see A-27, A-32, A-42, D-11, D-16, D-27, D-28, D-34, D-36, M-72, M-94, M-97, M-506, M-583, R-1, R-2, R-3, R-33, R-34, V-9, V-17, and Z-2 as examples.  M-91, M-630, R-10, R-17, R-60 and Z-4 are connected to some aspect of the puzzle as a whole rather than the words in them.   M-151 is a multiplication in which all of the words are not only coherent, they (just about) read out as a sentence.     Finding a frame in which all of the words are coherent and the keyword is in one of the standard orders is uncommon except for miniature puzzles, and sometimes occurs by exceptional luck: M-627 was not only the unique framing of the numbers generated, but also produced a key in a standard order (though with an unusual word).

You should always hand-solve any construction before submitting it for publication.   A good rule of thumb is that a puzzle should be able to be solved in less than an hour, and using no more than one sheet of paper.  I usually try to avoid problems where one of the letters is unclued: that is, it occurs only in an addition of the type A + 0 = A or A + 9 = A, and nowhere else.  This happens sometimes in additions, and much more rarely in divisions (a letter might pass from the dividend to the remainder (almost always in the units column, unless the quotient is one digit, as in D-55)).  Of course, its value can be found by elimination, but I find a problem less elegant when a value cannot be confirmed in any other way.  I generally like to avoid too many obvious clues: I rarely have zeros or ones in the multiplier or quotient, if I can help it, or as the last digit of the multiplicand (or divisor), unless the zero or one provides no additional clues.  These preferences are not absolute: if a problem has other merits (such as having many coherent words [see R-35], or even better, thematic ones), I might still use it even with some of these minor flaws.

Finding Cryptarithms via Computer Search

Puzzle Virtuoso

I have been developing an omnibus Windows program to help me in designing and solving many different kinds of puzzles.   This originally started as a program to solve domino logic puzzles.   I later added modules for solving various kinds of cryptograms (including simple substitutions and Vigeneres), and several kinds of logic puzzles including Castawords, sudoku, and latin square puzzles.  Many years ago I had written a set of cryptarithm functions in the APL language, for generating and framing addition, multiplication, division, square root, and interlocking equation puzzles in any desired base.  Some of these have been rewritten and adapted for Puzzle Virtuoso.  It also has functions to automatically compute multiplication tables and LDA tables for any base up to 30, a solver for additions with any number of addends in any base, and various search functions.

  IRRELIEVABLE   A-70   (2 words, 8153274096)
+ IRREVERTIBLE
  AFFINITATIVE

I have used a custom function, part of Puzzle Virtuoso, to look for cryptarithms with long coherent addends and sum.   The ideal puzzle above has two coherent 12-letter addends and a coherent 12-letter sum (all three words can be found in Webster's Second New International Dictionary (1948) and the Compact Oxford English Dictionary (1991)).   It works from a candidate list of words, and checks every pair of words (including duplicates) as addends, against every other word in the list as a possible sum.  It checks each possible puzzle (using the cryptarithm addition solver built into Puzzle Virtuoso) to find those with exactly one solution, and in which every digit occurs (the above example is in ordinary base 10, but the program can potentially find solutions in other bases such as 11 or 12, popular ones in cryptarithmetic puzzles): see A-80, A-90, and A-91.  The puzzle above was the only valid one turned up by a search of 651 highly-patterned 12-letter words (extracted from a raw word list from Webster's Second, herafter abbreviated as NI2).   The extraction was done with a different PV module which generates pattern word dictionaries, in this case with an option set to filter out any patterns shorter than 8 digits (the three words have patterns 12-22413743, 12-224325173, and 12-224351537).  Similar searches have been performed on shorter words (a similar list of 355 11-letter words generated 177,092 potential puzzles, but only 10 valid ideals).   One was published in The Cryptogram (C-13 in SO16, p.26); three others appear herein as A-71 through A-73.   (Just before publication I found the Word Ways article by Mike Keith which includes a number of discoveries up to 13 letters.  Rats.)

This search function can also be used to find thematic additions, using a selected list of words: see puzzles A-25 through A-35 for examples (some of these were found using an online search program, others with Puzzle Virtuoso).   Any candidate for publication needs to be hand-solved, as many additions do not solve well (relying on a lot of tedious brute force).   A curiosity which popped up while doing the search of checker opening names, which produced A-33, was the twin ideals DUNDEE + GLASGOW = DOUGLAS and DUNDEE + DOUGLAS = GLASGOW, but neither solved well enough to be selected.

Smallest Additions and Square Roots

A different kind of search looks for an ideal addition with the smallest possible sum.    The smallest I have found is the following:

   PLACE     A-8   (2 words, 1-0)
 +  DOOM  
   REDID

These puzzles are hard to frame, and very difficult to solve, but the puzzle above can be solved by hand by searching for zero and trying various cases (see the detailed walkthrough in Hints).  See Challenge Problem Z-11 for an example which might be too difficult for hand solution.

A computer search for the smallest ideal square root in base 10 produced the puzzle R-12; the smallest cube root appears to be R-35.    R-30 is the smallest square root in base 13, and the only one with a four-digit radicand (there are 57 in base 11 and 6 in base 12 [see R-25]).

Smallest single-digit multiplications

I wanted to find an ideal multiplication cryptarithm (with a single-digit multiplier), with the smallest possible multiplicand.   The equation ABCD x E = FGHIJ has 13 solutions, so I made a list of every possible multiplication with a five-digit multiplicand and five-digit product, with one repeated digit.   There are 55 possible multiplications; I copied each one into a multiplication solver (using Puzzle Virtuoso and two others).   Six of the multiplications have no solution, 42 have multiple solutions, and there are seven ideals.   Some might be too difficult for hand solution (but see M-606 in the Hints); they are problems M-601 to M-607 in order from smallest to largest multiplicand.   (I later found that Andree's book contains a different framing of one of the solutions.)

Divisions are much harder to search because of the larger number of combinations of dividend, divisor, and remainder. I have found several small examples by hand (D-10, D-12, D-20), but I am not certain whether there are smaller examples. D-12 is the smallest dividend I have found for any ideal division; D-20 is the smallest I have found with a single digit quotient.

Nine odd words

      When I first tried composing coherent additions, I used pattern word dictionaries to find pairs of words which looked suitable (and had letters in common), then tried to find values which produced a sum to which I could match a third word.  I was successful on occasion, and produced three cryptarithms which were published in The Cryptogram (C-14 JA97, C-8 JF98, and C-14 ND98).   When I wrote a search tool much later to look for ideal additions, I put the nine words (average, decoder, organdy, coolest, terrace, deports, octopus, scallop, results) into it to see if it would reproduce the three additions.  To my astonishment, it turned up all three, plus six additional cryptarithms using combinations of words from different puzzles (two of the six include a repeated addend).  In addition, there are 3 more ideals in base 11 and 2 in base 12.   I do not know if this is a result of selecting pattern words, or if many groups of 9 seven-letter words would produce similar results.   But it seems remarkable to get 14 valid puzzles from a list of only nine words.

Thematic Square Roots

    Another search tool in Puzzle Virtuoso looks for a square root by testing a range of values (for example, every five-digit number with a nine-digit square), and compares the pattern of the desired root to the pattern of the first (five) letters of its square.   This program, at present, needs to be customized for each run, and has other limitations.   Here is a live example I composed while writing this.  I wanted to find a square root cryptarithm with a solitaire theme, where the square root of STOREHOUSE is equal to DEMON.  I customized the program to check every possible value of DEMON with a ten-digit square (from 31624 to 98765) and check whether its square starts with a five-letter pattern (STORE) in which the E's and O's match, but no other digits are repeated.  This takes a minute or two to set up and a second or two to run.  It gave me a list of 9 possible solutions; I scanned by hand to see whether H could be assigned a value equal to or larger than the sixth digit of the square (three of the cases were unusable by this check).  I usually like to have roots without zeros, and that gave me the following cryptarithm (R-10: 2 words, 2061795483, give an appropriate key for this discussion):

      D E M O N
   V STOREHOUSE        R-10
      E
      NOR
      NRS
       NSEH
       TTUE
        NOTOU
        NDTOH
         HEENSE
         HMMDEN
          RRRRD

Creating the Problem First

A very difficult method is to choose the words you want to start with (these should be thematically related), then try to find numbers to make the calculation come out correctly.  This has been used most succesfully in additions, particularly using computer searches.  Additions of this type were a staple of the Alphametics section in The Journal of Recreational Mathematics.  Problems of this type almost never have a keyword, since it is unlikely that a random ordering of ten letters will form something coherent.   If you pick three words at random, it is very rare that there will be a unique solution, and many problems in JRM ask for the mininal solution or put some other constraint on the values (such as specifying one or more of the numbers must be prime).

A higher rate of success is likely with divisions, since the remainder can be juggled as described above. This method was used to create D-26, the cryptarithm appearing on the cover of WGR8.  Multiplications are even harder to work out, since they must come out exactly.

Interlocking Equation Formulas

In creating interlocking equations, it is desirable to be able to use a variety of formulas, ranging from the simplest, comprised of six additions or six multiplications, to complex ones with all four operations. Some sample formulas are given below. Select a formula, plug in numbers (of whetever length desired) for A, B, C, and D, and use the equations to compute the other five values. The last value, usually the largest, should be checked in both directions. Make sure that the nine numbers encompass all ten digits.  Some of the equations are self-working: nearly any values of A, B, C, and D will work (sometimes there are simple constraints).  Others, usually combining operations, have extra formulas for calculating one number from the other three. These are usually divisions, which must come out exactly: this puts extra constraints on the first three numbers selected.    It's possible to do a 4x4 with eight equations if you use all additions or all multiplications (see I-19, which has more of the feel of a magic square).

Self-Working Formulas

[1] A  +  B  =   A+B
    +     +       +         [I-17]
    C  +  D  =   C+D 
   A+C + B+D = A+B+C+D

[2]    A+B  -   A =   B                  
         /      +     +           (B-A) + (D-C) =  (A+B)   [I-15]
       C+D  -   C =   D                            (C+D)
    B+D-A-C + A+C = B+D         Note: C might be greater than D

[3]  E+D  / C+D-E  =  C           C and F both even        [I-14, I-20]
       -        +     +           G = C x (C + F)      D = (F + G)/2
     D+B  -     B  =  D           E = G - D
       A  + C+D-A  = C+D         then choose any A, B so that A + B = E

[4]  AB  /  A  =   B                C + D = (AB - A - B) / 2    [I-4]
      -     +      +                   A and B are both even.
      C  +  D  =   C+D 
    AB-C - A+D = B+C+D

[5]  A  x  B  =   AB                C = (AxB) - A - B    [I-2]
     +     +       +                          2   
   C+D  -  C  =    D                  A or B are both even
 A+C+D  + B+C = AB + D              (a slight variant of [4])

[6]   A x  B  =   AB               
      +    +       -
      C x  D  =   CD            (B-1)(A-1) = (C+1)(D+1)    [I-3]
    A+C + B+D = AB - CD

[7] AB /   A =  B                For *** to fit both equations,
     +     -    x                    D = A x B x (C-1)      [I-1]
    CD /   D =  C                         (B+1) x C
   *** / A-D = BC

[8]  A +  CD =    A + CD            (A-1) x (B-1) = (C-1) x (D-1)   [I-21]
     x     /        +
     B -   C =    B - C       
    AB +   D =  A + B + CD - C

Minimal Interlocking Equations

    OR +  T = UP            I-21
     +    +    +      (2 words, 0-9)
     A +  Y = OP
    US + OR = EM

The smallest ideal set of interlocking equations (with the largest number as small as possible) I've been able to construct is the puzzle above.

Magic Squares

Standard methods for creating 4x4 and 5x5 squares can be found in sources listed in the Bibliography. There is only one basic 3x3 square (with numbers 1-9): all solutions are rotations and/or reflections.   An NxN square can be multiplied by a constant value and another constant value added to vary the range and difference.  Most of the 4x4's herein were made by adding constants to each of the two squares below, multiplying each by different constants, and adding the two products together.  Constants used for many of the Q's herein are given in the solutions.

1 4 2 3      4 2 1 3
3 2 4 1      1 3 4 2
4 1 3 2      3 1 2 4
2 3 1 4      2 4 3 1
 Latin1       Latin2

Computing LDA tables

The tables used in leading digit analysis are not hard to construct for a particular base, given the corresponding multiplication table.  Either a whole table can be constructed, or individual values can be calculated on the fly,  Let's see how.

For short products, the table has entries for X (single digit) and Y (leading digit of long number) only when the product of X and Y is less than the base (for example, base 10 has values for anything times 1, 2 x 2, 2 x 3, 2 x 4, and 3 x 3).   The range of values runs from X x Y to one less than X x (Y + 1); for example, the maximum value for 3//2 is 8, one less than the minimum value (9) for 3x3.  If there are no values for the next value of Y (X x Y is larger than the base), the maximum value is 1 less than the base.  Examples:

(a) Base 10, single digit 6, long number beginning in 1.   Minimum value is 6 x 1 = 6.  There are no values for 6//2, since 6 x 2 > 10, so the maximum value for 6//1 is 9; the entry is 6789.
(b) Base 10, single digit 3, long number beginning in 2.   Minimum value is 3 x 2 = 6.   Minimum value for 3//3 is 9, so the maximum value for 3//2 is 8; the entry is 678.
(c) Base 11, single digit 5, long number beginning in 2.   Minimum value is 5 x 2 = a (ten in base 11).   There are no values for 5//3, since 5 x 3 > 11, but a is already one less than the base; the entry is a.
(d) Base 13, single digit 4, long number beginning in 2.   Minimum value is 4 x 2 = 8.   Minimum value for 4//3 is c (twelve in base 10), so the maximum value for 4//2 is b (eleven in base 10); the entry is 89ab.

For long products, each table entry is either one or two digits.  First put down the tens digit of the corresponding multiplication. Now check the product for the next higher leading digit (immediately to the right in the multiplication table). If the tens digit of this product is one larger than what you have already put down, and the product does not end in zero, put that digit down behind it.  Note that there is no entry in the long product table for A (single digit) and B (leading digit of long number) unless the product of A and B + 1 is greater than the base.

Base 10 Examples:

(1) single digit 6, long number beginning in 4.    6 x 4 = 24; put down 2. 6 x 5 = 30, ends in 0, so the entry is 2.
(2) single digit 7, long number beginning in 8.    7 x 8 = 56, put down 5. 7 x 9 = 63, put down 6; the entry is 56.
(3) single digit 4, long number beginning in 3.    4 x 3 = 12, put down 1. 4 x 4 = 16 (same digit); the entry is 1.
(4) single digit 6, long number beginning in 1.    6 x 1 = 6, put down nothing. 6 x 2 = 12; the entry is 1.
(5) single digit 3, long number beginning in 2.    3 x 2 = 6, put down nothing. 3 x 3 = 9; the entry is blank.

More examples:

Ideal Doubly True Cryptarithms (besides Additions)

In 1988, WGR Contest Eight asked for a doubly true multiplication in any operation except addition.   Leonard Gordon submitted the sole entry in January 1990, the problem below.  His problem does include one addition, but it is an excellent discovery, and I awarded him the contest prize (he selected Hugh ApSimon's Mathematical Byways in Ayling, Beeling, and Ceiling).   Len submitted it without partial products [the solution to (FOUR x NINE) + FIVE = FORTYONE is unique], but I added the first and last letters (and a mixed keyword) to make it reasonable to solve by hand, and it was published in WGR11 (June 1992, page 7):

     FOUR    M-841  (L. Gordon)
   x NINE  (2 words, 6548317920)
    Y***O
   T***V
  T***T
 T***V  
 ********
+    FIVE
 FORTYONE

     FOUR  M-92       THREE  M-107*
   x FOUR          x    SIX
     SXON            RHHXNN
   FXTRO            OTRRIS
  FIFSE            ETHIER 
  FOUR             EISHTEEN
  SIXUEEN         

Foreign Languages

     SEDM     M-842
   x  DVA    (3 words, 8315427069)
    ERDRT    
   EVCCC     
  CNAVR 
  CTRNACT

Here's one that works in Czech (7 x 2 =14), if you drop the diacritic marks (14 in Czech is čtrnáct).   The English keywords include an abbreviation.

Doubly True Roman Numerals

       XI               
     x XI              
      MCI               
     CLV                
     CXXI               

Appendix 1: An Annotated Bibliography

Magazines

The best source of cryptarithms in terms of quantity, quality, and variety is The Cryptogram (published bimonthly by the American Cryptogram Association; membership is $18 per year).  It publishes 90 or so cryptarithms a year (usually 16 problems per issue, plus a few extras, though one or two per issue are word sudokus rather than cryptarithms), ranging from additions to double-key divisions.  It is the only source I know that currently publishes square and cube roots, magic squares, double-key problems and cryptarithms in bases other than 10.  The entire run of the magazine (updated every five years) in PDF format is available to ACA members: a treasure trove that is closing on 6000 cryptarithm puzzles.

Some variety puzzle magazines (such as Dell Math & Logic Problems), which can be found on most newsstands, include cryptarithms.  A typical issue of Math & Logic Problems contains 45 divisions, under the title Word Arithmetic.  Dell's puzzles all have coherent dividend, divisor, quotient, and keyword, and are somewhat harder to compose than some of the divisions found in The Cryptogram (D-7 and a few other divisions herein follow that standard).  Occasionally additions and multiplications are also seen.  Most of Dell's divisions tend to be on the easy side, with values of 0 and 1 obvious in many problems.

The British magazine Tough Puzzles (still published) used to feature several types of cryptarithms, including incoherent multiplications by Jack Stubbington under the title Trying Times; I do not know if it still does (a recent issue I saw had no cryptarithms).  Games World of Puzzles (originally Games) also has occasional cryptarithms (see also the article by B. Upton-Rowley, "The Logical Cure For Digititis", in Games, March/April 1980).   Word Ways, the premier journal of recreational linguistics, is available online at the Butler College Digital Commons.  The current editor is Jeremiah Farrell.   Numerous articles on alphametics have been published there, including a regular column by Steven Kahan between 2015 and 2019.    Crux Mathematicorum, a Canadian publication, is also available online, courtesy of the Canadian Mathematical Society, and has published cryptarithms occasionally.

Several other magazines which published cryptarithms regularly are no longer being published.  The Journal of Recreational Mathematics (published quarterly by Baywood until 2014: the last issue was Volume 38, Number 2) published about 12 alphametics per issue, mostly additions.  Some of the problems (usually one an issue) were giant problems with ten or more addends.   Its predecessor, Recreational Mathematics Magazine, also published alphametics: the complete collection of these has been republished in a book by Charles Ashbacher (see below).   Cryptography, published bimonthly, had in each issue two dozen or so interlocking equations by Rocky Da Monduelli, under the title Cryptequations.   Puzzletopia published a number of miniature hidden cryptarithms by Dr. Ohkoma in issue 1 in 1985 (see Appendix 6 for two examples), a monster hidden cryptarithm by T. Kato in the issue 2 in 1987, and various alphametics in other issues.

Four-Star Puzzler featured a variety of cryptarithms, including hidden cryptarithms by B. Upton-Rowley under the title Digititis (nine issues), interlocking equations by Thomas K. Brown under the title Balanced Equations (issues 20, 22, and 27), and other cryptarithms by Sidney Kravitz, Mike Shenk, and others.   It was published by Games Magazine from January 1981 through August 1983 (32 issues).  It initially ran 12 pages, increasing to 16 pages beginning in January 1982.   Recreational Computing published a column on cryptarithms by John Davenport Crehore (ACA member Nine Hex), which ran for six issues during 1979 and 1980, with problems for solution either by hand or by computer.  Hints were given for many puzzles, and solutions appeared in the next issue.  Crehore earlier had a column called Cryptorithms in Mechanix Illustrated in 1941-1942.   All of the issues in both of his columns can be downloaded or read online at archive.org; see Other Articles below for details.

New Scientist (still published) included a puzzle for most of its history until December 21, 2013.   These originally appeared under the title Tantalizer (by Martin Hollis), later as simply Puzzle (by Eric Emmet, author of several puzzle books under his initials  E.R. Emmet (see below)), and finally as Enigma (by various contributors).   Over 2300 puzzles were published in all: a fair number of these were cryptarithms, ranging from completely hidden to conventional incoherent ones without keywords.   Some of Emmet's puzzles are notable as possibly the first examples of Topless Divisions: he gives the full dividends, so there is one more addition to work with, but the principle is the same.   Early incomplete examples appeared as Enigma 9 on April 19, 1979 and Enigma 41 on November 29, 1979; the first completes were Enigma 206, New Scientist 1352, April 7, 1983 and Enigma 380, New Scientist 1529, October 9, 1986.   He also had two incomplete multiplications with only the multiplicands missing (Enigma 263, New Scientist 1410, and Enigma 385, New Scientist 1534).  Both of these share the feature that the letters of the multiplier appear in the additions in such a way that a variation of the Hubbuber trick can be used to solve them quickly.   There are also examples of single-digit multiplications (easy incompletes) and additions with four addends.   Jim Randell's Enigmatic Code website has details on most of the New Scientist problems.

Ashbacher, Charles -- Alphametics as Expressed in Recreational Mathematics Magazine, 2015, self-published, 42pp., paperback, ISBN 978-1508538134
Recreational Mathematics Magazine, published from February 1961 to January-February 1964 (14 issues in all) was the forerunner of The Journal of Recreational Mathematics.  It was founded and edited by Joseph S. Madachy, several of whose books are also included in the bibliography.   This book is a complete collection of the more than 60 (mostly) alphametics which appeared in RMM.   Most of the non-addition puzzles are partially hidden cryptarithms, and there are two completely hidden ones.  Solutiuons to all of the puzzles are included.

ISBN 0-486-21039-1
154 problems and solutions, many of them from The Sphinx.  Methods are outlined for solving the first 46.  About half of the problems are partially hidden.   A good source for solving methods, particularly for hidden cryptarithms.

van der Elsen, Jack -- Alphametics, Cijferen met Woorden, 1999, Shaker Publishing B.V., 59 pages (PDF), ISBN 90-243-0084-1 [Dutch]
This is listed in several bibliographies and I looked for it for many years, finally buying a PDF copy directly from the publisher for 3 Euros (it is also available in paperback).  It is described as a dissertation; I don't know if that means for a university degree.   Small collection of addition alphametics with detailed solutions, including some discussion of modulo arithmetic, repeated decimals, and solving by computer.   Only one of the included puzzles is ideal, a well-known doubly true problem.

Jain, Hitesh Tikamchand -- ABC of Cryptarithmetic, 2017, All India Ramanujan Maths Club, 81pp., Kindle, ISBN 978-93-5311-257-8, $1.50
Collection of problems with solutions (mostly additions, but other types mixed in including multiplications and hiddens), and basic techniques.

   

Kahan, Steven -- Have Some Sums To Solve, June 1978, Baywood, 114+14 pp., paperback, ISBN 0-89503-007-1
Kahan, Steven -- At Last!!! Encoded Totals Second Addition, July 1994, Baywood, 123+14 pp., paperback, ISBN 0-89503-171-X
Kahan, Steven -- Take A Look At A Good Book, July 1996, Baywood, 121+8 pp., paperback, ISBN 0-85903-142-6

Steven Kahan, the long time Alphametics editor for The Journal of Recreational Mathematics (and later for Word Ways), published three collections of problems from JRM.  Have Some Sums To Solve (Baywood, 1978) has only 40 problems, but they are good ones, including 20 ideal doubly true alphametics (the book title itself is an alphametic, as are the titles of the two sequels).  Kahan gives some general hints on solving in the preface, then gives an excellent directed approach to solving each problem, suggesting a means of attack without filling in all the details.  This allows the stumped solver to have another crack at a problem, and helps beginners learn good solving techniques (most of these are multiple addend additions).   Solutions are given in a separate section.   The two sequels, At Last!! Encoded Totals Second Addition (1994), and Take A Look At A Good Book (1996), follow the same format, and also include a variety of interesting general puzzles and number curiosities.

Rea, Cyrus F. -- Cryptodigits, Volume 1, 2015, Klooto Games, 96 pp., paperback, ISBN 978-1516819737, $7.15
200 original addition and multiplication cryptarithms, all incomplete, unkeyed, and incoherent: I only counted four problems which contain even nine of the ten digits.  These are mostly miniatures: I didn't see any problems with a sum or product longer than six digits.  Many of the additions have three (and occasionally four) addends.   For the first 150 puzzles, blank crosstables are provided which show which digits are present (the same information is provided for the remaining 50 puzzles in a hints section).  A second hint (the value of one letter) is also available for each puzzles, and there is a section with full solutions.  The book is published in large format (three puzzles per page), with room to fill in solutions.  I like the format of the book, but would prefer to see ideal puzzles with keywords at least.   No second volume has appeared to date.

Sachar, Louis -- Sideways Arithmetic From Wayside School, 1989, Scholastic, 89 pp., paperback, ISBN 978-0-590-45726-2, $5.99
Children's story of a strange school.  The first four chapters present 24 alphametic problems for solution, including hints and answers.  The remainder of the book contains various kinds of logic problems.
Sachar, Louis -- More Sideways Arithmetic From Wayside School, 1994, Scholastic, 94 pp., paperback, ISBN 978-0-590-47762-8, $5.99
Sequel to the previous book.  The first ten chapters present 29 more alphametic problems for solution, including clues (directed methods of solution), hints (one correct value for each problem) and answers.   Only a few of the problems are ideals.

Mahmoha, Mme -- Numbers Behind Letters, 150 Fanny [sic] Cryptarithm Puzzles, Alpham3tic Puzzles With Solutions, 2021, self-published, unnumbered (165 pp.), paperback, ISBN 9798481279497, $6.66
Print-on-demand collection of 154 thematic addition cryptarithms (alphametics).  Each puzzle appears on one page with a crosstable to keep track of possible values for each letter.  More than half of the puzzles are incomplete (less than 10 letters); many have values assigned to one of more letters (sometimes to avoid multiple solutions).   The difficulty ratings (1 to 5 stars) are unreliable: the last puzzle, number 154, is rated 5 stars, but can be solved with direct entry.   Probably many were found using search programs, which can generate hundreds of puzzles from thematic word lists; a few of the puzzles have appeared in other sources which were independently generated the same way.   The introduction claims, without evidence, that the alphametic puzzle "seems to have been well known in India and China at least 1,000 years ago".

General puzzle collections which include cryptarithms

Some of these are still in print, available from Dover Publications.   There are many general puzzle books which have a few cryptarithms included: I have omitted most of these if only numerical answers are given, without detailed explanations.

Averbach, Bonnie, and Orin Chein -- Problem Solving Through Recreational Mathematics, 1980 W.H. Freeman, 2000, Dover, 458 pp., paperback, 0-486-40917-1
Chapter 5, More About Numbers, Bases, and Cryptarithmetic, pp. 145-172, covers the fundamentals of base conversion and computation, followed by a very short section on cryptarithms, analyzing SEND + MORE = MONEY and a mostly hidden cryptarithm from The Sphinx.  Pages 169-172 contain 64 sample problems.

Ball, W.W. Rouse, and H.S.M. Coxeter -- Mathematical Recreations and Essays, Thirteenth Edition, 1987, Dover, 418pp., paperback, 978-0-486-25357-0, $18.95
Wide-ranging collection of mathematical puzzles, originally published in 1892, and still in print.   Gutenberg.org has a digital copy of the Fourth Edition from 1905; archive.org has the Sixth Edition from 1914.  Brief section on Arithmetic Restorations, pp. 20-27, includes several hidden cryptarithms by W.E.H. Berwick (including the Seven Sevens problem) and others, and an incomplete cryptic division published in The Strand Magazine in 1921.  

Kraitchik, Maurice -- Mathematical Recreations, Second Edition, 1953, Dover, 330pp., paperback, ISBN 0-486-20163-5, $18.95
Originally published in 1942; still in print.  Brief section on Cryptarithmetic, pp. 79-83, mostly hidden and partially hidden.   His comments are odd: he mentions The Sphinx and Vatriquant's coining of the term cryptarithmie, but then says: "...problems of this sort were known earlier, and there are better examples in "La Mathematique des Jeux" (1930).  Here are two: ".   He quotes two problems published in 1929 in the Belgian chess magazine L'Echiquer, both hidden cryptarithms using chess pieces to represent the unknown digits.   The book he mentions is actually his own:  La mathématique des jeux ou Récréations mathématiques, Paris: Vuibert, 1930, 566 pages (note that this was published shortly before The Sphinx began).  Then he praises Pigeolet, one of The Sphinx editors, and gives six of his problems.   It sounds like he admired Pigeolet much more than he did Vatriquant.   It turns out that Kraitchik was the editor-in-chief of The Sphinx, and Pigeolet was the cryptarithm editor.

Knuth, Donald E. -- The Art of Computer Programming, Volume 4A, Combinatorial Algorithms, Part 1, 2014, Addison-Wesley, 912 pp., hardback, ISBN 978-0-201-03804-0, $79.99
Discussion of algorithms for computer solution of alphametics on pp. 324-325 and 332-333.   A number of problems are presented (21-31 and 34, pp. 346-347, solutions pp. 706-707), mostly additions; some of these have computations on both sides of the equal sign.    Also includes some pandigital puzzles (see the book's index).

Langman, Harry -- Play Mathematics, 1962, Hafner, 216pp., hardback
I bought a very battered, dirt-cheap copy of this.  It includes chapters on Letter Divisions (pp. 52-62) and Skeleton Divisions (pp. 63-69)  Several regular and hidden cryptarithms are analyzed, and more than 50 additional problems are given (including rarely seen hidden square roots), but there do not seem to be any solutions included!   On pages 52-54, he analyzes an easy division in great detail, pointing out almost everywhere there is a clue and constructing a nearly complete greater-than-less-than chain. The section on Magic Number Arrangements (pp. 70-106) does not mention cryptarithms, but is a good survey of magic squares and many other shapes with magic properties.  It also includes more than 100 problems, but again without solutions.   I wonder if this was originally meant as a student guide, with a teacher's edition (with solutions) published separately.   It was reprinted in paperback in 2012, but that edition is the same length as my copy.

Lewis, Frank (R. Masterton) -- Problem Solving, Part One, 1989,  Nation's Best Puzzles, 112 pages, paperback, $9.95
The section on cryptarithms, pp. 66-72, gives step-by-step solutions for a division and a square root; a multiplication is included in the supplemental problems.

ABC -- Adventures in Cryptarithms (Or Through The Digital Maze With Gun And Camera), The Cryptogram, July-August 1963, pp.130-131
Analysis of a division with a three-digit dividend and divisor.

Fire-O -- A Tool for Cryptarithmaticians: Multiplicative Structures, The Cryptogram, May-June 1970, pp. 45 (front cover), 47, 63
Analysis of chains of last digits of multiplications.   Also described in Crotalus's book.   Fire-O gives his own sample problem, and also suggests that the method can be used on his C-10 from MA61 (the same problem attacked by Fiddle using leading digits in his JA61 article).

Crotalus -- A Cryptarithm Observation by Hubbuber, The Cryptogram, November-December 1973, p.127
Brief note about Hubbuber's trick of finding extra additions (also described in Crotalus's book).

Pit -- Cryptarithmic Crutch, The Cryptogram, July-August 1980, page 75
Table of all values for two internal additions of the form A + B = C and A + C = D, with all possible carries.

Crotalus -- Make Your Own Arithmetic Tables in Other Bases, The Cryptogram, May-June 1989, pp. 3-5, 31
Shows how to construct addition, multiplication, and multiplicative structure tables in other bases; includes them for base 13.

Fomalhaut -- Leading Digit Analysis for Cryptarithms, The Cryptogram, July-August 1991, pp.8-9
Explanation of leading digit analysis for both short and long products, with two solved examples, and tables for bases 10, 11, and 12.

Apex Dx (and Crotalus) -- Solving SO98 C-Sp-1, The Cryptogram, January-February 1999, page 5
Two of the ACA's cryptarithm experts gave their methods for solving my Topless Division (C-Sp-1, SO98).

Apex Dx -- Master of the Cryptarithm Remembered, The Cryptogram, September-October 2005, pp. 4-5.
An assortment of puzzles by Hano, selected by Apex Dx.   A couple of these are found in the Mu Alpha Theta article below, but most are not.

GGMA -- Rapid Solving of Cube Roots by a Pattern Method, The Cryptogram, November-December 2007, pp. 4-6.
Excel spreadsheet functions to allow searching for patterns in partial powers.  Includes two base 15 problems, a cube root and a fourth root.

Fomalhaut -- Solving AC-1035, The Cryptogram, September-October 2014, pp. 4-5.
My analysis of a difficult set of base 19 cryptarithms (three additions and a multiplication with a single key) by Apex Dx in the JF13 issue, which appeared in the Analyst Corner rather than as a Cryptarithm special.   The table of possibilities on page 5, unfortunately, is incomplete, missing a few cases.

Fomalhaut -- Finding One in Square Roots, The Cryptogram, November-December 2014, p.8
My explanation of the principle of flush-left remainders in square root cryptarithms.    Includes a base 13 square root as an example to be solved.

Other Articles

Yoshigahara, Nob, ed. -- Puzzle World, 1992, Ishi Press International, 64 pages.
Intended to be a regular publication, but the premier issue was also the only issue.   It includes many alphametics.

Magic Squares
Andrews, W.S. -- Magic Squares and Cubes, 1917, 1960, Dover, 419pp., paperback, ISBN 0-486-20658-0, $5.00
Benson, William H., and Oswald Jacoby -- New Recreations With Magic Squares, 1976, Dover, 198pp., paperback, ISBN 0-486-23236-0, $4.00
Benson, William H., and Oswald Jacoby -- Magic Cubes, New Recreations, 1981, Dover, 142pp., paperback, ISBN 0-486-24140-8, $4.00
Moran, Jim -- The Wonders of Magic Squares, 1982, Vintage, 227pp., paperback, ISBN 0-394-74798-4, $5.95

Other Bases
The Dozenal Society of America
Non-profit organization for the promotion of base 12, founded in 1944 as the Duodecimal Society of America (there is also a British counterpart). Their website has many interesting articles, in PDF format, on notation, as well as calculation, in base 12 (see below).   There is also an archive of back issues of The Duodecimal Bulletin.

Haas, Victor E. -- The Magic Numerals of Ali Khayyam, The New Mathematics Made Easy, 1965, Macrae Smith, 155 pp., hardback
Entertaining children's story about a young boy who wins a round-the-world trip in a breakfast cereal sweepstakes.  The trip leads to a series of adventures (including a shipwreck and being kidnapped by pirates) in which Ali learns to do arithmetic in base 2, 5, 8, and 12.   I first learned about bases as a child by reading this book.  Almost 150 exercises in converting between, and computing in, other bases, with solutions.

de Vlieger, Michael Thomas -- Multiplication Tables of Various Bases
Tables for bases from 2 through 60.  Most of the tables use a set of numbers called argam, of de Vlieger's own design, though the base 11 and base 12 tables use the Dozenal standard numerals, and there is also a hexadecimal table in standard ABCDEF notation.  The article is 44 pages long, but page 1 contains the most frequently used tables from base 2 through base 12.

de Vlieger, Michael -- Symbology Overview
History of the notation for base 12 numerals, starting with the rotated 2 and 3 proposed in 1857 by Isaac Pitman (of shorthand fame).  Later script X and E were proposed; today DSA uses script X and rotated 3 in its publications (following the recommendation of pioneer typographer William Addison Dwiggins).

Schiffman, Prof. Jay -- Fundamental Operations in the Duodecimal System
Good explanation of doing addition, multiplication, and long division in base 12.   Understanding the principles will allow you to do arithmetic in any base.

Workman, W.P., assisted by R.H. Chope -- The Tutorial Arithmetic, Second Edition, 1903, University Tutorial Press, 553pp., hardback
Comprehensive early 20th-century textbook on arithmetic, including the oldest hidden cryptarithms I am aware of (problems 30-37, pp. 48-49; problem 1, p. 480).   Chapter 34, Scales of Notation (pp. 460-469), covers computation in other bases, including over 75 problems, with solutions.

Programming

Barlow, Mike, ed. -- Cryptogram Computer Supplement, number 4, 21 pages, 1987, The American Cryptogram Association
All 22 issues of CCS are available as PDFs for free download to ACA members from their website.   The fourth issue is devoted to cryptarithms, and includes a bibliography (continued in CCS 5) of nearly every article The Cryptogram had published to that date on cryptarithms.

Appendix 2: Supplementary Problems

Problems marked with * are fully worked out in the main text.

Additions

A-1 (2 words,9-0)  A-2 (3 words,1-0)  A-3 (3 words,0-1)
  GRAINSILO           HOUSING           NIAEE   VIOLA
+ GRAINSILO         + HOUSING         + PIANO + PIANO
  BGNLSPARI           MAORHRS           VIOLA  SNSWNN

A-4 (2 words,     A-5 (2 words,     A-6 (2 words,
   3947216580)      1394752086)      2861075394)
    STEPUP            MISREAD          PRAIRIE
  + CHURCH         +  ADDRESS        + HABITAT   
   APPRISE            SCENERY          CHIPPED

A-7 (2 words,     A-8 (2 words,       A-9 (2 words,
  2015374698)           1-0)           4825670931)
   LATERAL             PLACE             DEFEAT
 + EVASIVE           +  DOOM           +  STILL
   SQUARES             REDID             EXTRAS

*A-10 (2 words,  *A-11 (2 words,     
  2739015846)      4509732681)        
    NASAL              VIPER           
    DUETS               PANS
  + LUNGS            + REDIP
    TREAD             SALINE

[chess openings]   [chemical elements]  [solitaires]     [checker openings]   [flowering plants]
  A-30 (3 words,     A-31 (2 words,    A-32 (2 words,        A-33 (2 words,     A-34 (3 words,
   9374508621)        9201346587)       8501946273)           9372861504)        6302895741)
   TRAXLER               COPPER           BRISTOL               NAILOR             FENNEL  
 +  VIENNA            +  SILVER         +  NESTOR            +  WAGRAM           + LUPINE 
   CATALAN              SILICON           OSMOSIS              GLASGOW             DAHLIA

   [moons]          [pianists]
  A-35 (2 words,   A-36 (2 words,
   2315840976)       1263749508)
    TITANIA             LISZT
  +  MANAKA        +  LIPATTI
    IAPETUS           PERAHIA  

Fibonacci Sequences

I introduced this as an addition variant to The Cryptogram: my first attempt was published in July-August 2017 as C-Sp-1 (it's pretty easy).   It's a series of additions: starting with the third word, each word is the sum of the previous two (if the first two words are the same length, the second is not necessarily greater than the first).  This is really a minature version of puzzles often seen, where the sum and difference of two words are given (A-3 above could be written as a Fibonacci: NIAEE PIANO VIOLA SNSWNN).   The examples below use shorter words and usually a longer chain.   A common theme in solving these is finding the possible values of the smallest of the leftmost column of leading digits (e.g. L in A-40 and P in A-43; see the Hints for more detail).   Another theme is finding one or more values for letters in the same addition in the units column and working in either or both directions to find the remaining values (see the Hints for A-60).   Search for zero can also be helpful (see the Hints for A-55 and A-65).  A-41 is a short chain which takes quite a bit more work than most of the longer chains (A-55 is also harder than most).

A-40 (2 words,  A-41 (2 words,  A-42 (2 words,   A-43 (2 words,
   1-0)            9-0)          8725946310)      2039651874)
     OH            TWO             AGO               ARM
    LIP           ECRU            SHIP              PROS
    APT           DATA            SPAR              ALSO
    PRY           WETS            HIGH              MUST
    SAT                           GIST              TOME
                                 TAPER

Undecimal (Base 11)
A-50 (2 words,    A-51 (3 words,
 a7541863029)          0-a)
     IS               EAR
     PI               RUB
     EX               YET
    OOH              IRKS
    ONE              TACK
    WAS
    CHI

Duodecimal (Base 12)
A-55 (3 words,    A-56 (3 words,
    0-1)              b-0)
    ASK              HOT
    GIN              AIM
    FRO             LYRE
   DAFT             LEAP
   DUDS             BETA

Tridecimal (Base 13)
A-60 (3 words,     A-61 (3 words,
    1-c)            bc6a240185739)
    BUN                HOW
    NIT               ONLY
    LOB               CARE
   CAFE               LEFT
   ORDO               ROOM

Tetradecimal (Base 14)
A-65 (2 words,     A-66 (2 words,
49c56d083a1b72)    9815b3cd640a27)
     THE                DEFY
     SUN                THAN
    AWAY                OURS
    AIMS               PROOF
    WOOD               POSIT
    SELL

Extra Long Additions

A-70 (2 words,
    8153274096)
  IRRELIEVABLE
+ IRREVERTIBLE
  AFFINITATIVE

A-71(2 words,     A-72 (2 words,     A-73 (2 words,  A-74 (2 words,
  2961754038)       0683742159)       0157432869)      3059741628)
  BARBARITIES       ECLECTICISM       POSTPONENCE     PROPRIETIES
+ PEPPERINESS     + VELVETINESS     + PHOSPHATESE   + POMPOSITIES
  RECRESCENCE       CONCOCTIONS       SCIOSOPHIST     REPRESENTED

Base 11 (Undecimal)

*A-80 (2 words,    A-81 (2 words,
   641932a8750)     236791405a8)
   UNFOUNDERED         ALOES
 + COINCIDENCE         BOOTS
   INSTITUTION         MATEO
                     + OAKUM
                       RUSES

Base 12 (Duodecimal)

A-90 (2 words,      A-91 (2 words,
   2830B6a49715)     5209B38741a6)
   LIMELIGHTER        SEMISEPTATE
 + CRABCATCHER      + TALETELLING
   ORTHOTECTIC        INTUITIVISM

Base 13 (Tridecimal)

A-100 (3 words,    A-101 (2 words,
 b179a564238c0)     ca96b72513048)
  UNLAUNDERED        UNCOUNSELED
+ UNPLUNDERED      + INTUITIVIST
  LIMELIGHTER        OUTPOPULATE 
 

A-200  Digimetic  (each digit represents a different digit)
   473584
+  242986
   716570 

D-1 (2 words,    D-2 (2 words,   D-3 (3 words,   D-4 (2 words,
  0986571324)    4637251980)      1204567893)     5269874301)
        PP                  HO             NO              I
TEND)LOOSE        GLOSS)RESEED   CANIT)BETRUE    STOMP)OMITS
     TEND               GLOSS          RNCAN           ROPED
     PASTE              SLIOOD         AONUEE           MOBS
      TEND              SNIIER         ANOTAR 
      SLID               HERON           BAOU

D-5 (3 words,   *D-6 (2 words,     D-7 (2 words,       D-8 (2 words,
  2603145897)          1-0)              0-9)               1-0)

                          AE                  NAP             RUST
          L    RAKLP)RESTATE   STRANGE)APOSTROPHE    MOLT)TUNGSTEN
 MALT)AWARD          RSTLRU            AGOENPTS           TTOMG
      ADMIT           RLPSEE             REOPTEH           GEUNT
       STOW           RURUPS             STRANGE           NLLRG
                       TYUTR             GHSGOPNE            LSGE
                                         NTASPRON            MOLT
                                          GPTHPTS            SGGUN
                                                             SOLUO
                                                              SMES

D-9 (2 words, 0-1) D-10 (3 words, 9-0)  D-11 (2 words, 0-9)  D-12 (3 words, 1-0)
              AH           TO                    NU                 TO
 TALENT)THIRTEEN       AN)DPS             PSI)PUTON              A)TRY
        TRREEEK           IN                  PATP                 IN 
         IKANAAN           IS                  ATPN                 MY
         NTNRNXE           EM                   NAU                 ME
          HIKIRE           AS                   AEL                  D

D-13 (3 words, 1-0) D-14 (3 words, 1-0)  D-15 (2 words, 0-9) D-16 (2 words, 0-9)
         ME                    ON                   GO                    US
 PROM)VERSE          TMMDE)INDIGO          TALK)GROTTO        TOPICS)POLITIC
      SRVO                 RMMNO                NNPKO                TOPICS
      MVMME                DNDEBO                LOGAO               UJUYOOC
      MAPAV                DOMMTR                LKKOI                IJYOLP
        VTI                 DDEMT                 NRKI                TJYYYP

D-17 (2 words,    D-18 (2 words,        D-19 (2 words,    D-20 (2 words,
   9150327846)      6427815093)           0-9)              0-9)

            S                  T                  O              I
 SELLS)ENIGMA        STEAM)HOMER         REED)COMMA         OX)SAW
       ALTARS              BEARD              CLOSE            TEN
        ASALG               MMSS               AHSC             AD

D-21 (3 words,    D-22 (3 words,        D-23 (3 words,   D-24 (3 words,
         1-0)         1-0)                2378640159)         9-0)

           HE               O                       T                   O
   LINT)ATONE       OATH)ALSO           OTDTSE)INDOOR     ARELLNT)INTEGER
        LINT             SOLE                  HARASS             RNLOGIT
        HHHTE             NVI                  OAINEO             LSGOIRO
         IYIN                 
         LSHA

D-25 (2 words,       D-26 (2 words,    D-27 (2 words,     D-28 (2 words,
       0-9)           7360259184)        7409581362)             9-0)
           KKSSR              ERIE                 EU                 P
KOALA)KOOKABURRA    HURON)SUPERIOR      PLUTO)ESOSNLS     DEIMOS)PHOBOS
      AURUEU              SOPHU               SATURN             PBASEI
       ABEOSU              PNUEIO              URANUS             OHHDM
       AURUEU              PNRHTI              EANATA
        SLARLR               SNPPR              STSOU
        UEBYUY               SOPHU  
         SSOAUR               ENSE
         UEBYUY
          BRYLUA
          BBLAYA
           OSOAL

D-26 appeared on the cover of WGR8, slightly modified here to produce more thematic keywords.  It was inspired by Mike Shenk's "Continental Divide" from The Four-Star Puzzler, May 1982.

D-29 (2 words,    D-30 (2 words,      D-31 (3 words,    D-32 (2 words,
        0-9)           0-9)            9012345678)        7814590362)
           NOR                  OUT            DUMP                FIVE
 GONGS)SONGMAN    PRUNING)ALLIGATOR   RTMI)PRETTIED     THREE)SEVENTEEN
       RSOUR              GOAOITN          PEREU              SRSREN
       ACUCOA             NUIGGORO          TUEMI              SHSEVE
       AGRHCN             NRGUUNIP          TPPMD              SFVVNI 
        NMCSHN             NONNPRNR          TIKRE              NRVAIE
        NMCONS             NPOITIAT          TMURT              RFFSHI 
           ORO               AIGOPL           ETISD              VTTIIN
                                              EKMRS              VTSHHE
                                               TPPU                 IIE

D-33 (2 words,   D-34 (2 words,   D-35 (3 words,  D-36 (2 words,
       1-0)           0-1)          1239708456)      7568934012)
        US                   R               A             F
 ERE)DELIS      CIRRUS)CUMULUS   AXIMRS)REHASH    TUNA)TROUT
     DBNO              CDGRUMR          OHRIHM         TRTDF
      NNOS              SCOSLD          HORRID           EEL
      NNRI 
        RO

D-37 (4 words, D-38 (2 words,    D-39 (3 words,   D-40* (2 words,
       0-9)          1-0)          1539247806)      6452970318)

           G               S               K              N
 POINT)TWANG      OOPS)STILL      SHED)CRIED      MEOW)TRAP
       ANPSE           ELONR           CHECK           WONT
       NGWIA            ONNU            AALI           MALE

D-41 (2 words,  D-42 (2 words,   D-43 (2 words,    D-44(1 word, 
     0-1)         4310275968)     9631024578)            1-0)
        YIS              FRY             ZINC               PEP
 AYE)ARTERY       FRO)MALADY    IRON)CHROMIUM      PLOT)SCHOOLS
     AAEP             OOMO           COMCH              EHPSL
      TBAR             FASD           HURRI              HEECL
      EYME             FIOO           HOCHN              TITNT
        YMY             YYRY           UUCNU              SLNPS
        AYE             IORL           UZIIH              EHPSL
        AIR              FLY            MICMM              ELCH
                                        MZHMI
                                         CRGU

D-44 was one of the sample problems in WGR8.   It was the first Dell-style division I ever composed.

D-45 (2 words,    D-46 (3 words,   D-47 (2 words,     D-48 (2 words,
  9516023478)       4187306952)      7265043189)          1-0)
         ME                CC               ON               LIE
 MANY)THOSE        EASY)WITCH      PART)PRAISE        YIN)ARMLET
      ASHT              TEST            PINTO             ALEI
      LYONE              WISH            PARVE             LARE
      LEYOT              TEST            PRAIR             NRRN
        ALL               TWO             PAST              YMIT
                                                            LIDI
                                                             LID
D-49 (2 words,    D-50 (3 words,   D-51 (2 words,    D-52 (2 words,
    0-1)              9-0)          6918732504)       1806273954)
        AT                   B              PI               IF
 SOB)URIEL       FORAGE)RADIOS       INS)PHYLA        ONE)SEEMS
     BEOT               REIGFB           ASKS             SONS
      OTLL               EBEEF            KKPA             LENS
      OTTA                                KEEP             LOAF
        BE                                 PHI              IMP

D-53 (2 words,    D-54 (2 words,   D-55 (2 words,   D-56 (2 words,
  0642935781)       9128470536)     4213689507)       9410275368)
            RE              TE                 Y               E
 SPACE)EXPORTS     LORE)PIRATE      FRISK)BELFRY   OMECCO)CARESS
       EPORIC           PEIPP             BRIBES          ALCOVE
        TSARES           PROBE             BLURS          OLPOSC
        TSXEOI           PLATE
          SXCR            STOA

D-57 (2 words,    D-58 (2 words,    D-59 (2 words,  D-60 (2 words,
    0-9)            9053247681)      3490186257)      8269130754)
      OF                  EH                AS               IT
 AS)FERN           TRY)ANGUS         NOW)EXIST        RED)UDDER
    FIE                NEAT              EASE             USES   
     CAN                EARS              ATRT             OOFR
     CEV                EYSA              ATEN              FOR
      IF                 RUN                ES              TIN

D-61 (2 words,    D-62 (2 words,    D-63 (2 words,   D-64 (2 words,
 4382765019)        4891675302)        3528079416)    5014897236)
       IT                 NO                IN              BY 
 ION)LAME          HAD)SHORT         POI)LOUPE       ABS)ACIDS 
     EAT               SIRS              LETS            ARIA 
     POSE               HUNT              PATE            ALMS 
     PLEA               HUSH              PLEA            ALAR 
      PAL                 AS               LAP              AD 

D-65 (3 words,     D-66(3 words,   D-67 (2 words,    D-68 (2 words,
   0-9)             5483207961)      2146093785)      3268519074)
         E                  I                 L                 C 
 HERA)SHAY         LIEF)AWFUL      EMAIL)GLEAMS       CHASE)PRIDE 
      DROP              AMITY            GAUGED             PERMS 
       PAN               FLEW              VIAL               SPA

D-69 (2 words,     D-70 (2 words,   D-71 (2 words,   D-72 (2 words,
  4652783091)        1745928630)        0-9)          9251067483)
        MA                 ME               ON                AN 
 TAX)TAILS          SIR)PRUNE        SOP)UNDER         TWO)SNARE 
     THAT               POEM             UDFA              SHOE      
      THIS               SOME             SDOR              HOSE 
      TOME               SURF             SRFU              HAWS 
       TIL                 ES              USE                TI

D-73 (3 words,     D-74 (3 words,   D-75 (2 words,   D-76 (2 words,
     0-9)               0-9)          8152947063)         9-0)
        ERA               HIS               OPT              ALE 
 IRE)HAUNTS         DEW)SHEAR        NIX)PLANET       DAM)REALMS
     HHEA               IHT              PANT             RSLD   
      FRIT              NSWA              ANTE             RRRM  
      FFSE              NIDD              APTN             OEML  
       ESUS              DHTR              EXLT             DDYS 
       EEAU              DDNE              ERAO             DPDR 
        IFN               NIN               EAN              DOY 

D-77 (2 words,    D-78 (2 words,   D-79 (2 words,   D-80 (2 words,
   5479386012)     3218957640)      6193547082)        0-9)
           B                 S                E              I 
  VAST)INSET      ADITS)ENCASH     TURBO)REACTS     RILE)GOERS 
       ABOVE            ENTIRE           RECODE          LITHO 
        IRON              TENS              ARC           LORD

D-81 (3 words,    D-82 (2 words,    D-83 (2 words,  D-84 (2 words,
  1596472038)      0129634578)       8104673925)     1370459286)
          S                 I                 T              L
 USER)STOCK         OVER)SENT        RISE)RAPID    APHID)SHALE 
      CARDS              SHOP             SOUPS          SAITH
       CUTS               PRO              PURE           READ 

D-85 (2 words,    D-86 (2 words,    D-87 (2 words,  D-88 (2 words,
 0675149328)        5086149273)          0-9)        5903624718)
         AM                AN               SO              ME
  OPE)TEMPS         SHE)MATTE        SET)GOUDA       AGE)HUMOR
      TANG              MENS             GNCU            HELM 
       OWES              FAME             SNEA             OUR  
       ONTO              FILM             USCN             SHO 
        APE                IT              GDO             HAH 

D-89 (2 words,    D-90 (2 words,   D-91 (3 words,   D-92 (3 words,
  4762150893)      4260398157)          0-9)            0-9)
             D               I                E                F 
 COPIES)SCARED     NEARS)DECKS     SALON)BODIES     BLEAT)ARTILY
        RECOUP           OCEAN           AEBLST           ABYRIU 
         ERCOA            SIDE            ATEID            YFTBI

D-93 (2 words,      D-94 (3 words,  D-95 (2 words,  D-96 (2 words,
    0-9)              5204736918)     5638497201)        1-0)
               I               F               D               W
 MARIMBA)TIMPANI     WORKS)RIFTS     IDEAS)SALVE    BAFTA)TRICOT
         TIIETRI           SATIN           STRAY          TOSIOS 
            BNOP           KNOWN            DEAL           FITST

D-97 (2 words,   D-98 (2 words,    D-99 (2 words,  D-100 (2 words,
   5921786430)        0-1)           3915276804)        0-9)
          OF               TO              ANY             LIE
 TILE)SOFTLY       REDO)ITEMS        OLD)NOVEL       AIL)DOERS
      STAYS             EPTX             VOE             NID 
       TTSIY            SEOTS            OSAE            RSDR   
       TLTTO            SPMPD            AIYO            RAGI 
        LIAR             TRDP             LDLL            AAGS 
                                          LYIY            AOAS 
                                           LAV             ASO 

D-101 (3 words,  *D-102 (2 words,  D-103 (2 words,  D-104 (2 words,
     0-9)           8705612493)      9270638514)      6325901748)
            P                 N              G                 K
 RAYED)DEPART      AVERT)ADVERB     FAIR)GENTS      OAKEN)OHSERK
       APRSTI            ABOEAD          ARGOT            OOHTWO
        DSMYE             RANTS           TRIO             THAWS

D-105 (2 words,   D-106 (2 words,  D-107 (3 words,  D-108 (2 words,
      9-0)          8906427135)      0943281756)      9317604825)
           H                 Y                U               H
   AUTO)RUST      OPERA)TRYEND     UNCAP)FUGATO     NASTY)CHORE
        RACE            TORNAY           FLAGON           RECON
         HEY             TOWER            NFGCA           ENACT 

D-109 (2 words,   D-110 (2 words,
    0-1)              0-9)
           UH             ES 
 MULTI)BEATLE      HIS)CLEPT 
       ULHAE           CHPI 
       MMEMIE           CCST 
       MMUBWU           PLIL
         BIIL            HAO

D-113 (2 words,   D-114 (2 words,  D-115 (2 words,  D-116 (2 words,
  5106379284)       4031258769)       7642930158)     9367082541)
           I                 T                 U               L
 HABIT)WATCH      DEMOS)MAJORS      SOUND)RAPIDS     SOLID)WEIRD
       WANTS            MAYEST            ROINSU           WORST 
         TUB              MEAD             USING            FLOW

D-117 (2 words,
   6812907534)
          N 
 READ)NOISY 
      ANGER 
       ROAD