Puzzle Laboratory Guide to Domino Logic Puzzles


Every combination occurs 3 or 4 times; the solution is unique

In 1874, O.S. Adler developed a domino game with a double-7 set (36 pieces), which he patented in 1893 in Germany as Dominosa (under the pseudonym Richard Osa).   He wrote a book on it in 1894, and later collaborated on another book with the noted game collector and writer Fritz Jahn.   I have looked at both the patent application and the book (see Bibliography); the 1921 edition is available on archive.org.  It's not clear to me, with my very limited German, what the patent is for, or whether a deductive puzzle was the main intent (most of the diagrams show constructions similar to quadrilles), although the book does have one 9x8 rectangle and a solution.  Nevertheless, the name Dominosa has been adopted by some sources as the name for the puzzle.

The Gent's Game can serve as the basis of a number of construction tasks involving the frequencies with which the 28 domino combinations occur within the 97 adjacent pairs of the 7x8 rectangle. Of course other sets and rectangle sizes can be used as well.  Here are three problems and example solutions (the solution to each array shown is unique), which appeared in WGR7. Improvements, examples for other sets (especially double-9 and double-12), and new ideas are welcome.

(1) Arrange the 28 dominoes so that a given double or non-double occurs a maximum number of times. In diagram 1, 6-6 occurs ten times while 0-1 occurs twenty-one times.
(2) Arrange the dominoes so that the largest number of combinations occur only once (on the domino that contains that pair). In diagram 2, 14 combinations occur only once.
(3) A variation of (2) counts only the non-double combinations which occur exactly once. This is more challenging than (2). In diagram 3, there are 12 non-double pairs that occur only once, while every double combination occurs at least twice.

                 
                 Diagram 1                                           Diagram 2                                           Diagram 3        

This record was shattered by the array below, which has an astonishing 730,924 solutions!  Remarkably, every one of the 97 possible domino positions is possible except one: the 1-2 domino cannot be placed at bc5.



German Gonzalez-Morris improved this further, to 807,752 solutions.  In the array below, every possible position is found in at least 35,082 solutions.


            807752 solutions

The 28 combinations will always have a total frequency of 97.  But what are the largest and smallest possible products of their frequencies? The largest, it turns out, is (3^15)*(4^13), which is solved by the diagram at the beginning of the article.  The smallest product should have as uneven a distribution as possible, with many combinations with frequencies of 1 and 2, and a few with very large frequencies. For example, it might be possible to have four different double combinations occurring 10 times each (as 6-6 does in Diagram 1), or two non-doubles occurring 15 times or more. What is the lowest possible product?  On the back cover of WGR12 there appeared a modification of Diagram 1 from that article (shown below).  In addition to 6-6 occurring 10 times and 0-1 occurring 21 times, 16 combinations occur only once, and the product of the 28 frequencies is 853,493,760.  I worked the array out on October 4, 1997: the solution is completely trivial.

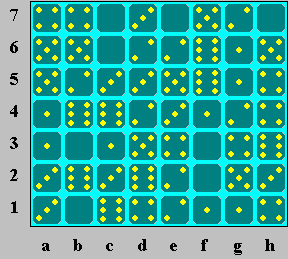
Dissected Dominoes -- Solving domino logic puzzles

The grids have been labeled to help make the solutions easier to follow.

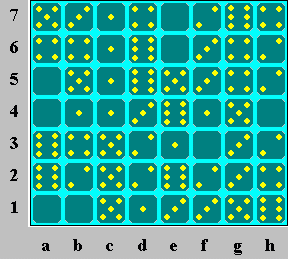
Problem 1: There are only two possible places to put the 5-5 domino; both use the 5 at c2, so it cannot be part of a 2-5.  The only other place for the 2-5 is at cd3, so the 5-5 must be at c12.    The only place left for the 2-2 is at h56, forcing the 4-6 to be at gh7, and the 6 at h1 must be part of 5-6 to avoid duplicating 4-6.  If the 0-6 were at a12, there would be no way to pair the 6 at a3 without duplicating either 0-6 or 4-6, so the 0 at a1 must be part of 0-0.   If the 0-3 domino were at ef6, 0-2 would have to be at ef7, forcing the 0 at h4 to be part of 0-5 (to avoid duplicating 0-2), and the 0 at a5 to be part of 0-4 (to avoid duplicating 0-0 or 0-5).  But then 3-5 would have to be at ab7, and there would be no way to pair the 5 at e5 without duplicating 3-5 or 5-6.  So 0-3 can only be at fg3.  The only place left for 0-1 is ab4, and the square at ab12 must be divided into 2-4 and 6-6 to avoid duplicating 4-6.   The only place left for 0-6 is at de6, and the 5 at e5 must be part of 3-5, forcing 4-5 to be at a67 and leaving g56 as the only place for 4-4.    2-3, 0-4, and 0-5 are forced, leaving h34 as the only place for 0-2, and forcing 1-5 and 3-4.  Now there is only one place for 3-3, and 1-2, 2-6, and 1-6 are forced.  3-6 must be at d45, forcing 1-1, 1-3, and 1-4. 

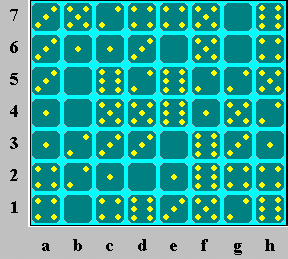
Problem 2: Avoiding duplications

If the 5-5 domino were at f67, it would leave bc4 as the only possible place for 0-5, and then g67 as the only possible place for 0-0.  4-6 would have to be at h67, and 0-4 and 4-4 would use the fours at a1 and e7 in either order.    Then the fours at c1 and h2 would both need to be part of 1-4 to avoid duplicating other dominoes, so either 1-4 or some other domino would be duplicated.    So it is impossible for 5-5 to be at f67, and it can only be at cd4.   Now if 0-5 were at fg7, then the only place left for 4-5 would have to be h56, and the six at h7 would be isolated.   So 0-5 must use the five at f6, 4-5 must be at ef7,  2-5 must use the five at h5, and the only place for 5-6 is at f12. 0-5 cannot be at fg6 (forcing 0-6 at gh7 and a duplicate 4-5 at h56), so it is at ef6.

Parity

The only location left for 6-6 is e45, and if the blank at e3 were part of 0-1 or 0-3, it would divide the unused area into two parts, each with an odd number of squares.  Those regions could not be divided into a whole number of dominoes (which must add up to an even number of squares), so the arrangement is impossible.  This principle is called parity -- every unused region must contain an even number of squares.   So 0-6 must be at ef3 (dividing into two even regions), and 0-0 at g67 (avoiding duplication), which forces 4-6 at h67.    Now 2-6 must be at gh12 to avoid duplicating 4-6, and the six at c5 can only be part of 1-6, which forces 2-3 and 2-4.  3-6 must be at de1, forcing 0-1 and 3-3.   Since 3-3 has been placed, the threes in column a must form 3-5, 1-3, and 0-3.    1-1 and 0-2 can only be at a34 and b34, and the two at b2 must be part of 1-2, forcing 0-4 and 4-4.  2-2 must be at fg5, and the remaining dominoes are easy to place.

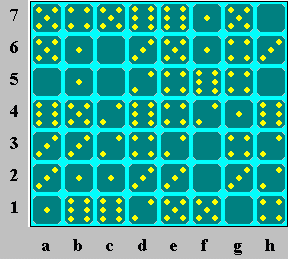
Problem 3: If the 6-6 domino were at de7, the six at b1 would have to be part of 6-1, and 6-2 would be at cd1 to avoid duplication.  But then the six at d4 would have to be part of 6-4, and the six at f5 would duplicate one of the three dominoes already placed.   So 6-6 is at bc1, 3-1 is at a12, and 1-1 is at bc2 to avoid duplicating 3-1.  5-5 cannot be at ef1, because 3-2 at d12 and 3-0 at ef2 would force 4-3 at g23 and a duplication with the three at h6.  So 5-5 is at a67, and f1 must be part of 5-0, so 3-0 is at h67.  1-0 cannot be at bc6, because 5-4 at bc7 would force 5-1 and fg7, and the one at b5 would duplicate 1-0 or 5-1.  So the one at b6 must form 4-1 at b67.  6-5 must be at cd7 (we already know 5-0 is at f12 or fg1), forcing 6-1 at ef7 and 5-4 at g67. 0-0 must be at c56 to avoid duplicating 3-0, and ab5 is the only location left for 1-0.   Other dominoes must be placed to avoid duplication: 6-3 at a34, 5-1 at ef6 (forcing 3-2 at d56), 5-3 at b34, and 5-2 at de1. The only remaining location for 4-4 is e45, and 2-1 can only be at fg4, forcing 6-4 and 6-0. 6-2 must be at cd4 to avoid duplication, forcing 4-2, 3-3, and 2-0. 2-2 can only be at h23, and the last three dominoes (4-0, 5-0, and 4-3) follow.

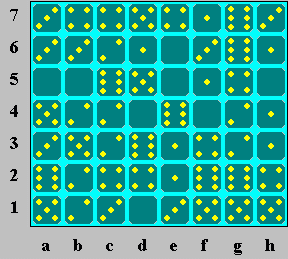
Problem 4: 6-3 cannot be at a23, since 5-2 would then be at ab1, and duplicated with the 5 at b3. Therefore either the 6 at g7 or the 6 at g6 must be part of 6-3, and 6-6 must be at fg2.  The only places for 5-1 are d56 and d67, and either the 1 at h3 or the 1 at h4 must be part of 2-1, so 1-1 must be at e23. 5-3 must be at a34 or ab3 (since 6-3 is not at a23), so 3-0 must be at de1. This forces 5-5 at fg1 and 5-4 at h12, so 5-1 must be at d67 to avoid duplicating 5-4. 2-1 is not at gh4 (otherwise it would force a duplicate 2-1 at gh3), so it is at gh3, and 1-0 is at h45. This forces 4-0 at f34 and 4-2 at g45, and 4-1 must be at ef7 to avoid duplicating 4-0. Since 6-6 is already placed, 6-3 must be at gh7 and 6-1 at gh6. Since 3-0 is already placed, 3-1 must be at f56, forcing 0-0 at e56, 6-0 at de4, and 6-5 at cd5. 0-0 and 3-0 are already placed, so 5-0 is at a45 and 2-0 at b45, forcing 2-2 at c34 and 6-4 at d23.  The only place for 5-3 is ab3, and the only place left for 4-4 is bc7, forcing 3-3 and 3-2 in the upper area, and 4-3, 6-2, and 5-2 in the lower area.

Problem 5: 5-4 cannot be a67, since there would be no way to place the 5-5, so 4-4 is at ab7. 0-0 must be at c67, since 4-0 must use the zero at f3.

Making an assumption

What happens if 2-2 is at e12? The four at d1 would have to be part of 6-4, and 4-2 would be at gh4, since 4-4 and 6-4 are elsewhere.  4-0 could not be at fg3, since the region blocked off in the lower right would consist of seven squares and could not be covered. 4-0 would have to be at ef3, and 6-3 at h23 (since 6-4 would be at cd1 or d12).   6-3 would force 4-1 at gh1 and 5-4 at g23, which would make it impossible to use the four at h5 without duplicating either 5-4 or 4-1. So 2-2 is not at e12, but at de6.    Making assumptions about possible placements and checking the consequences is usually necessary in solving harder domino puzzles; sometimes you must go quite far along before finding a contradiction.

Since 2-2 is at de6, 3-0 is at de7, and 3-3 is at a12 to avoid duplication.  6-3 cannot be at c45, since 3-1 would have to be at c23 and 6-4 at either gh3 or h34 to avoid duplicating 6-3.  But then 6-0 would have to be at bc1 to avoid duplicating 6-4, and once again an area of odd size (nine squares) would be walled off on the left side.   Since 3-3 is already placed, the three at c5 must be part of 3-2 at bc5, forcing in turn 5-5 at ab6, 5-1 at a45, 1-0 at ab3, and 6-6 at bc3. Since 5-1 has been placed, 3-1 is at c23, forcing 6-0 at b12 and 6-4 at cd1.  The only place left for 6-3 is h23, forcing 4-1 at gh1. With 4-4 and 4-1 placed, 4-2 must be at gh4 and 5-4 at h56.  This forces 2-0 at gh7, 6-5 at f67, and 1-1 at g56. Since 5-4 has been placed, 4-0 must be at fg3 and 5-0 at fg2, forcing 2-1 at ef1.  3-2 has already been placed, so 5-2 is at d34 and the rest of the dominoes (6-2, 4-3, 6-1, and 5-3) are forced.

The complete solutions:

Bibliography

Copyright ©2024 by Michael Keller. All rights reserved. This booklet was edited most recently on June 10, 2024.