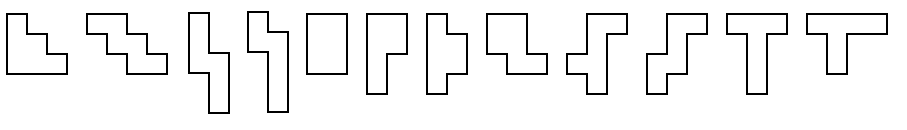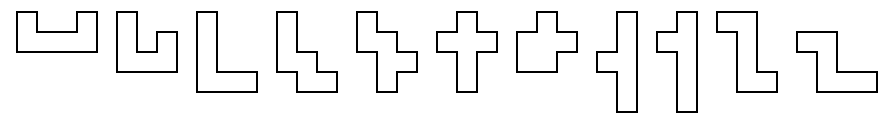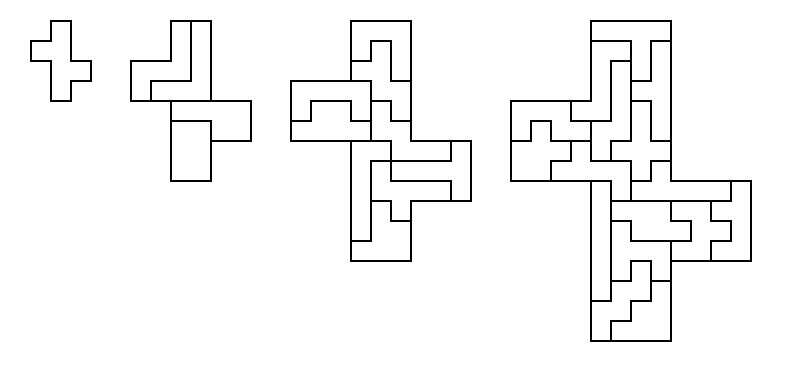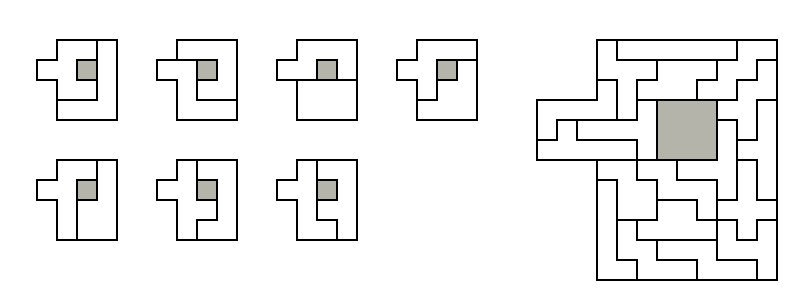Puzzle Laboratory Guide to Hexominoes
                               compiled by Michael Keller


  A    B    C    D    F     f     G    H    I   J    K    L



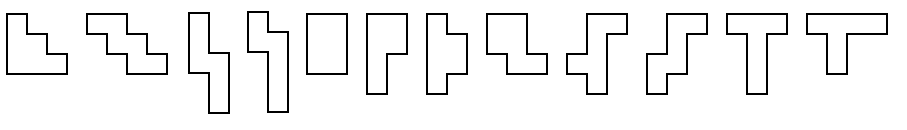
     M      m     N   n   O   P   p     Q    R     S     T     t  


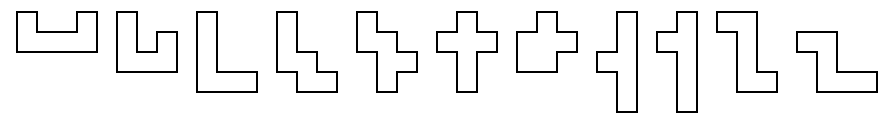
  U      u     V     W     w     X    x     Y    y   Z     z

                                                    The 35 Hexominoes

Special thanks are due for contributions to this compilation to: Andrew Clarke, Roel Huisman, George P. Jelliss, Henri Picciotto, Michael Reid, George Sicherman, Teun Spaans, and Anneke Treep.

The hexominoes (order-6 polyominoes) are a set of geometric shapes made up of six squares joined edge-to-edge in every possible shape.   Discounting rotations and reflections, there are 35 shapes as shown above.  We will use a single-letter notation, using a selection of upper and lower-case letters, to refer to the pieces throughout this booklet.  {I have reversed the designations of N and n from the original, as I wanted to follow the principle that, in pairs using the same letter, a capital letter denotes a symmetric piece and the corresponding lower case letter an asymmetric one, where possible, as with TUYZ.}  Before Solomon W. Golomb coined the term polyominoes in 1953, they had been studied largely in the pages of the Problem Fairy Chess Supplement (renamed Fairy Chess Review in 1936) under the title Dissections.  These constructions were mostly published in a condensed notation, rather than in full diagram form (which would have been prohibitively expensive in the 1930s and 1940s), and were little-known until G.P. Jelliss painstakingly decoded them and published them in diagram form in his journal Chessics (now available online).  In fact, the first dissection problem in the PFCS was by Herbert D. Benjamin in 1934, who correctly counted what are now called the 35 hexominoes, and proposed, in a Christmas puzzle with a 20-shilling prize, trying to form a 14x15 rectangle.  A year later, F. Kadner gave the now-familiar proof (using checkerboarding) that perfect rectangles cannot be formed with the full set, and was awarded the prize.   In 1937, Benjamin produced the first full-set construction without holes, the isosceles right triangle (problem [89] here), and G. Fuhlendorf produced a series of eleven 17x12 rectangles, each omitting one of the 11 unequal rectangles.  In 1946, Frans Hansson sextuplicated each of the 11 unequals, using a full set plus an extra copy of the piece being multiplied.  In 1947, he solved the 1-3-5 Problem (problem [95] here) for each of the 11 unequals, and finally in 1952, Hansson solved the problem of making 5 identical layers of 7 pieces with the full set (The Layer Problem, [82] here).  There is no record of the reverse problem, 7 layers of 5, having been solved in FCR.   Many other early constructions can be found in Jelliss' page on hexominoes.  Hexominoes were first mentioned by name in Golomb's 1965 book Polyominoes.   But even more than half a century later, they are very much overshadowed by their smaller cousins, the pentominoes.  This booklet is an attempt to show the scope of puzzles possible with the much larger set.

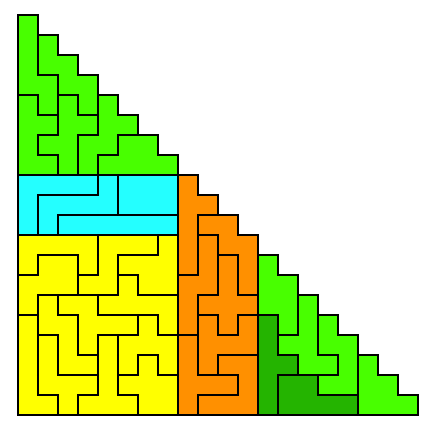
The majority of this booklet was originally published in WGR6 (September 1986) as WGR Special Supplement Number 1: New and Not-So-New Hexomino Puzzles, at the time the largest collection of hexomino problems ever published.  It has been supplemented here by additional material from other issues of WGR.   This supplement contains over 100 problems, most of them either new ones or new variations of older ones.  The nontrivial problems presented here are labeled with numbers enclosed in square brackets [11].  Solutions to selected problems are included.  However, many of these problems are open-ended (the best solution is not known).  Nearly all of the solutions here were found without computer assistance, except where stated, and for those few puzzles for which the total number of solutions is enumerated.



I was first introduced to hexominoes through Multipuzzle, a set of 48 hexomino puzzles published by Spear's, an English game and puzzle manufacturer.  BoardGameGeek says the first edition of Multipuzzle came out in 1960 (my copy of the booklet is undated); though it is out of print, copies can be found on eBay and other sites.  Multipuzzle comes with 42 plastic hexominoes (7 are duplicates: IMmPUuX) and a plastic tray 6x10 squares in size.  Each puzzle consists of a list of eight, nine, or ten pieces which are to be formed  into a 6x8, 6x9, or 6x10 rectangle (one or two I hexominoes are used to mark off a 6x8 or 6x9 area within the tray).  Solutions are provided for all puzzles. Of course, the pieces can be used for other hexomino puzzles as well: I found some of the older solutions in this booklet using Multipuzzle.  Shown above is a stylized map of my home state of Maryland, illustrated using the standard set of 35 pieces from Multipuzzle (using my over-half-a-century-old set).

A few comments on solving hexomino problems may be helpful.  The most useful rule of thumb is to place the difficult pieces as soon as possible and save the easy pieces as long as possible.  Here is a rough ordering of the hexominoes (from hardest to easiest to handle, and divided into five groups) which will be useful in most problems: KXwmZUuT  JARFzf  tHCGNWS  VIYnLy  DOpPxMQB.  In many of the solutions herein, you can see that the more useful pieces were saved until last (e.g. I found a solution to [70] moving generally left to right.)

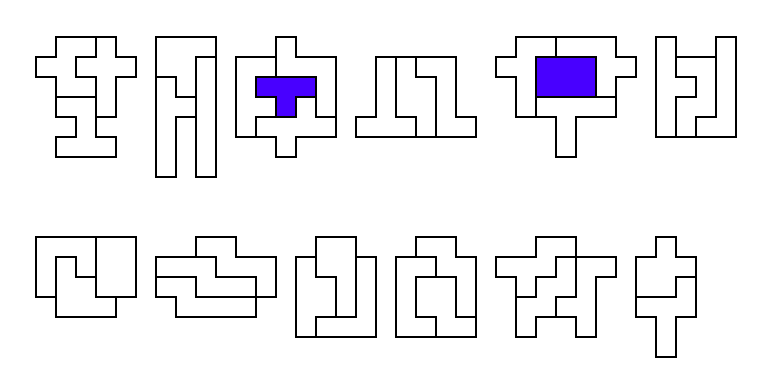
An important concept to understand is checkerboarding.  Imagine a figure to be solved being checkered black and white, and the hexominoes also checkered black and white. Twenty-four of the hexominoes, called equal hexominoes, cover 3 black squares and 3 white squares.  The remaining eleven, called unequal, cover 4 black and 2 white squares, or vice versa.  Therefore any figure which is to be covered by a full set of hexominoes cannot have an equal number of black and white squares; there must be two extra squares (or two plus a multiple of four) of one color.   For example, checkerboard the figure shown for problem [88], and you will count 104 squares of one color and 106 of the other color.  

So no perfect rectangle can be covered by the full set of hexominoes, and a subset of the 35 hexominoes can only form a perfect rectangle if it has an even number of the unequal hexominoes.   The smallest rectangle that contains the full set is 4x53, with two missing squares of the same color (see below):

When solving figures with a large difference between black and white squares, care must be taken.  For example, figure [89], the Pentagon, has a difference of 18 squares.  This means that 10 of the 11 unequal hexominoes must cover four squares of the majority color, in this case, the squares of the same color as the diagonal border (10*4+2=42, 10*2+4=24).   Below is a figure with the maximum possible color difference of 22.



For some of the subsets in section 1, a rectangle which is not perfect can be determined to be the best possible if a perfect rectangle is ruled out by checkerboarding and the intervening areas are ruled out by lack of suitable factors.  For example, in subset [34], a rectangle of area 63 is the smallest possible.  60 is ruled out by checkerboarding, 61 is prime, and 62 has only 2 and 31 as prime factors (too narrow for most pieces).

When trying to make long narrow rectangles, the length of the border is important.  If the pieces involved do not have enough border squares, the rectangle will be impossible to make.  Generally the number of border squares needed is twice the length of the long side.  The short ends are unimportant, as pieces placed at the corners can make up the extra length.  Perfect rectangles of width 3 are impossible with a full set of 35 hexominoes, as certain pieces (AFfHJQRStWXxz) divide the strip into two groups of squares which are not multiples of six.  The following list gives the usual maximum number of border squares for each piece. 

piece  A B C D F f G H I J K L M m N n O P p Q R S T t U u V W w X x Y y Z z
border 2 3 4 3 2 3 3 3 6 2 1 5 3 2 3 4 3 4 4 2 1 2 3 4 4 3 4 2 2 1 2 5 5 2 3


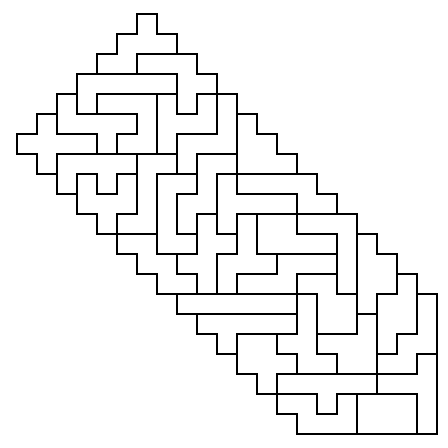
Contest Number Four: Hexomino Double Challenge (WGR4, February 1985, p.16)

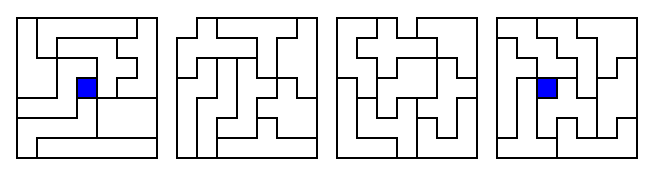
[1] Four hexominoes may be assembled into a 5x5 square with a hole in it. The hole may occur in any of six essentially different locations, as shown in the diagram below. (All other locations are rotations/reflections of the six basic squares below.) Use 24 different hexominoes out of the set of 35 to make six simultaneous 5x5 squares, each square having the hole in a different position.

[2] The second part of the contest is to solve the six squares above using as few different hexominoes as possible. In this part of the contest a hexomino may be used in as many different squares as possible (but not twice in the same square). Below is a sample entry, which uses a total of 10 different hexominoes (AfGKLMPUWY).   It should be very easy to beat this.  [Several solvers, including me, managed to get it down to five, which is the smallest possible because of parity.   See my solution with LMQUW in the Appendix.]

Variations suggested in the contest wrap-up in WGR5:

[3] Make four 7x7 squares with holes in different positions, using 32  pieces.

[4] Make as many 4x5 rectangles as possible with pairs of holes in different positions.  My best was 9, using 27 pieces, with two internal holes.  Roel Huisman improved this to 10, using 30 pieces, with no internal holes and all ten shapes sharing a hole in the upper left corner.



Hexomino Multiplication Problems (originally More Hexomino Problems, problems 1-6 on page 8 of WGR5)

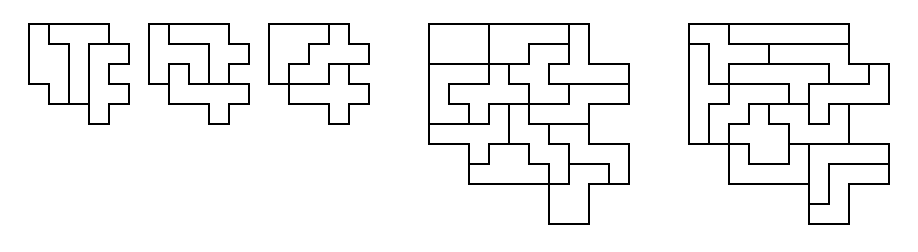
For those who enjoyed working with hexominoes (currently my favorite puzzle), here are some more problems to solve. A multiplication is a polyform construction in which an enlarged replica of a small figure (usually one or two pieces) is constructed using a selection of the remaining pieces.  Each single square is replaced by an NxN square.  For example, a duplication of the Q hexomino and a triplication of the w hexomino are shown below.  Note that the piece being multiplied should not be used in the larger figure, and when doing simultaneous multiplications, no piece should be used twice, including those being multiplied (the exception to this is that a piece being sextupled should be used twice more in the larger figure, to make 37 pieces in all).



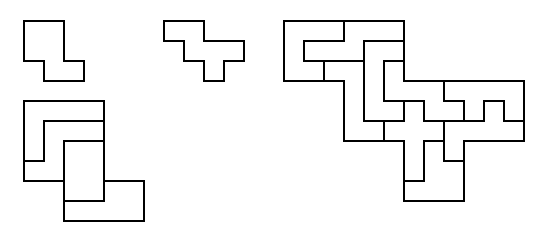
Two of the pentomino problems in Sivy Farhi's Pentominoes deal with multiplications.  The first is the double-double problem: Make a shape with two pentominoes,  make the same shape again with two more pentominoes, and finally make a double sized version of the same shape with the remaining eight pentominoes.  The second is the simultaneous triplication problem (solved by R. W. M. Dowler in 1980):  Construct a triple sized replica of each of the twelve pentominoes,  using nine complete sets of pentominoes (108 pieces).  Do not use any pentomino in its own triplication.  Farhi gives five solutions to the first, as well as Dowler's solution to the second.   Simple duplications (four pieces), triplications (nine pieces), quadruplications (sixteen pieces),  and quintuplications (twenty-five pieces) of single pieces are possible with the hexominoes, but all but the last are fairly easy, and quintuplications are only moderate in difficulty.  More challenging puzzles can be devised by doing simultaneous multiplications.  Remember that the piece or pieces being replicated cannot be used to duplicate other pieces (except when doing a sextuplication using a set plus one repeated piece).  These puzzles are listed in the order of the total number of pieces required (a very rough estimate of difficulty).

[5] Triple Triple (total 24 pieces): select two pieces and form them into a two piece shape, then make the same shape with two other pairs of pieces.  Finally do a triplication of the same two-piece shape using eighteen of the remaining twenty-nine pieces.
[6] Quintuple duplication (total 25 pieces): duplicate five hexominoes at the same time using twenty of the remaining thirty pieces.   [In the original article, I said I suspected that it is impossible to duplicate six (30) or seven (35) pieces.   George Sicherman has confirmed by computer search that this is the case: there are no solvable sets of six (30) pieces, obviously making seven impossible too.]

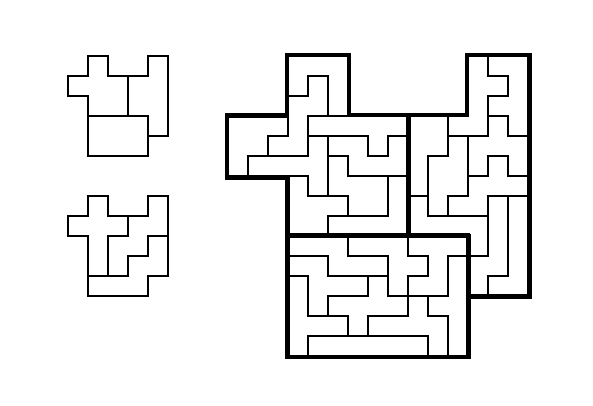
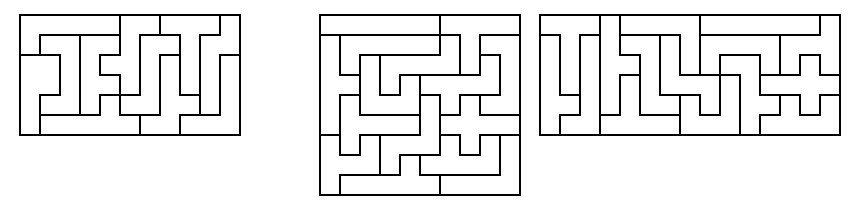
[7] Triple triplication (total 30 pieces): select three hexominoes and then triplicate all three at the same time using twenty-seven of the remaining thirty-two pieces.   (In WGR9 I extended this slightly, as seen above, by using three of the other pieces and making the same shape twice singly, then triplicated, for a total of 33 pieces).


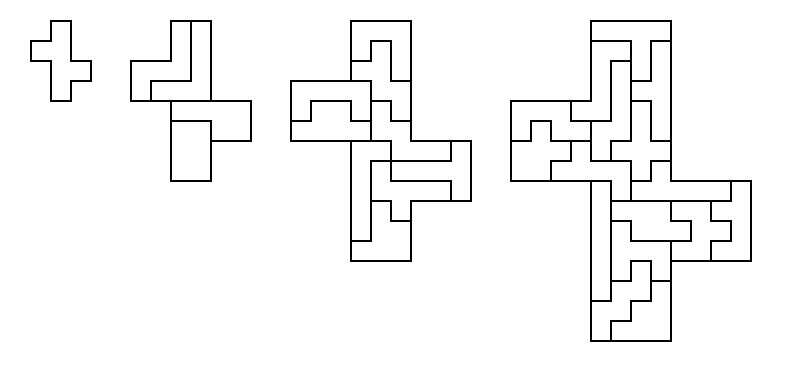
[8] One-Two-Three-Four (total 30 pieces): select a  hexomino and duplicate, triplicate, and quadruplicate it, using no piece more than once.  This problem was posed by Andrew Clarke in the Journal of Recreational Mathematics (13:1), for a mixed set of the 25 polyominoes of perimeter 12.  It is well suited to the hexominoes.  [In the original article, we asked whether One-Two-Three-Four-Five-Six is possible using 91 of the 105 heptominoes.   It is; Roel Huisman sent an example, shown below:)




[9] Double Double Triple (total 33 pieces): select three pieces and form them into a three piece shape, then make the same shape with two other triplets of pieces.  Duplicate the three-piece shape using twelve of the remaining twenty-six pieces, and finally duplicate the three-piece shape again using twelve of the remaining fourteen pieces.   [The appendix shows my solution where all of the three-piece shapes are composed of unequal pieces.]


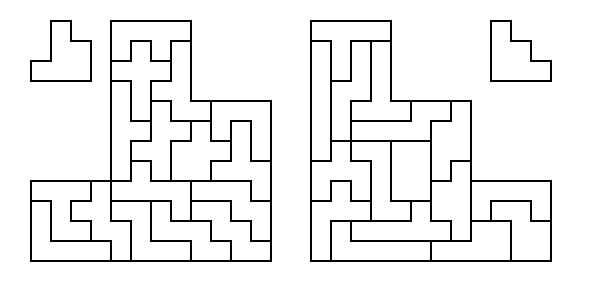
[10] Double quadruplication (total 34 pieces): select two hexominoes and quadruplicate both at the same time using thirty-two of the remaining thirty-three pieces.


Subset puzzles

Some puzzlers feel that the full set of 35 hexominoes has too many pieces to make a good puzzle.  It should be obvious from this booklet that I do not share this view, but there have been many puzzles derived from a subset of the hexominoes, and there are certainly interesting problems to be found among them.     H.D. Benjamin was perhaps the first to make constructions with subsets of the hexominoes.  His problem 4143 in the December 1939 Fairy Chess Review discards the 8 pieces which fit into a 3x3 square, leaving 27 pieces (CDFfGIJKLmNnPpRSTtUVWwXYyZz).   He uses these to construct a perfect 6x27 rectangle (Walter Stead later did 9x18).   T.R. Dawson constructed hollow rectangles with the 20 asymmetric pieces (problem 7593, FCR, April 1948).   Frans Hansson used the 24 equal hexominoes to construct a quintuplicated version of X with a hole in the shape of X placed symmetrically (similar to the full-set sextuplication below in [99]),  This was problem 10,201 in August 1955, and was followed later by similar constructions for other unequals.    In the June 1956 issue (problems 10,451 through 10,453), Walter Stead defined the 13 line pieces (set [40] below) and the 14 tree pieces (ACFfHJKRTtwXYy), and made perfect 6x13 and 6x14 rectangles respectively, as well as 9x18 with the combined set of 27 (which is the same as set [32] below).

Volume 14, Number 2 of the Journal of Recreational Mathematics included a problem (number 1064) by Harry L. Nelson : There are 11 hexominoes (FJKmNRSTwXZ) which can be folded into a cube.  What is the smallest rectangle into which they can all be packed? Nelson and Richard I. Hess each produced a 7x11 rectangle: this may or may not be the best solution.  In any case, we can produce other subsets of the 35 hexominoes and ask the same question.   Let us start by looking at the hexominoes which contain a 2x2 square.  There are eight of these (BDMOPpQx), all of which can be produced by adding a square to a P-pentomino.  We may thus call these P-derivatives [15].  Since there are three unequal hexominoes in this set, a rectangle of 6x8 or other dimensions is impossible.  Thus the smallest rectangle must have an area of at least 49 squares.  Is a 7x7 square (with one hole) possible? The answer is yes, and there are four locations possible for the hole, as determined by parity constraints.  All four locations (below) are solvable (a sample solution for the second location, the easiest of the four, is also shown). 


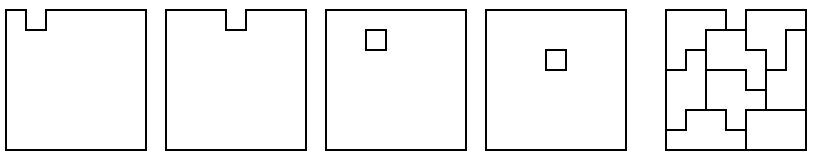
      11 solutions               22 solutions              11 solutions                5 solutions

                         The four 7x7 squares possible with the P-derivatives

Eleven other similar subsets can be derived, one from each of the other 11 pentominoes.  The pieces and the smallest rectangles possible for each subset are listed below.  (The trivial case of Xx is not numbered).  Michael Reid and Robin King found improvements for several of my original solutions.   George Sicherman recently analyzed the problem in Tables 1-4 by computer, finding several more improvements and proving all of the other results optimal.   Unusually for polyomino problems, a few of these rectangles have unique solutions (marked by underlines), disregarding reflections and rotations: [12], [19], [21], [22], and [37].

Table 1: Minimum Rectangles for Pentomino-Derivative Subsets

           Pentomino Derivatives   Rectangles
[11]  F    ABFfJKQwx                 7x9  
[12]  I    ILYy                      2x13    Robin King
[13]  L    CFLnPRTUVyZ               6x11    Michael Reid
[14]  N    DfGJNnPSWw                7x9  
[15]  P    BDMOPpQx                  7x7 
[16]  T    BHJTtX                    6x7  
[17]  U    ACGHOu                    3x13 
[18]  V    fMtuVz                 4x10, 5x8
[19]  W    MmQWw                     3x11 
      X    Xx                        4x5  
[20]  Y    CFKPpRtXYy                7x9  
[21]  Z    HQRSz                     5x7     Robin King

If you try dividing a hexomino into two trominoes, you will get one of four results: two straight trominoes (e.g. n), two right-angle trominoes (e.g. m), one of each (e.g. L), or you cannot divide it into two trominoes (e.g. A).  In two cases (D and O) you get either two straight or two right, depending on how you choose to divide it.  We can therefore produce four subsets, which I call  di-orthotrominoes, di-rectotrominoes, di-heterotrominoes and non-bisectable hexominoes.  We ask the same question: What is the smallest rectangle which contains every member of a given subset?

Table 2: Minimum Rectangles for Tromino Subsets

     Di-Tromino Subset  Pieces           Rectangles
[22] di-orthotrominoes  DINTV              3x11         George Sicherman
[23] di-rectotrominoes  CDGKmOpQRSUwxZ  4x22, 8x11     
[24] di-heterotrominoes BfHLMnPuWyz        6x11         Sergio Stanzani
[25] non-bisectable     AFJtXY             6x7
[26] tridominoes        ABFGIJLmNnO        6x23
                        PpQStUuVWYZz   

Instead of dividing hexominoes into two trominoes, what about dividing them into three dominoes? This is possible with all but one of the equal hexominoes, K being the exception. The remaining 23 tridominoes can be made into a 6x23 rectangle [26]. 
We can also divide each hexomino into a domino and a tetromino.  There are five tetrominoes, so we can generate five more subsets.  Note that K cannot be divided in this manner, but many of the hexominoes can be divided in more than one way, and thus fall into more than one group.  The S3 group is the same as the unequal (4-2) hexominoes. 

Table 3: Minimum Rectangles for Tetromino Subsets

   Domino Plus Subset   Pieces               Rectangles
[27] S1 tetromino (I)   ILnPptV                4x11    
[28] S2 tetromino (L)   BFGJLNOPQStUuVWYZz  4x27, 6x18, 9x12    
[29] S3 tetromino (T)   CDfHMRTwXxy         7x10, 5x14 
[30] S4 tetromino (N)   ABFGmnpQSW             7x9     
     S8 tetromino (O)   OPQ                    4x5     

Andrew Clarke's article Isometric Polyominoes in The Journal of Recreational Mathematics (13:1) discusses the perimeters (border lengths) of various sets of polyominoes.  The hexominoes fall into three groups: (1) O alone has perimeter 10, (2) seven hexominoes have perimeter 12 (the remaining P-derivatives), (3) the remaining 27 have perimeter 14.  The latter two groups (listed below) make useful subsets (O forming a trivial 2x3 rectangle).  We can also classify the hexominoes by number of sides.  I and O are rectangles (4 sides); L, P, and V are hexagons (6 sides); 15 hexominoes are octagons (8 sides); 10 are decagons (10 sides); the remaining five are dodecagons (12 sides).  The latter three groups are listed below (IO make a trivial 3x6 rectangle, and LPV make another easy 3x6 rectangle, this one perfect).  Some other possible subsets are also listed below.  The single path subset consists of those pieces which do not contain an S3 tetromino.  The S1 second derivatives are those pieces which consist of an S1 tetromino and two monominoes in any arrangement (this includes all of the pieces of [27]).  The N-less subset consists of those pieces which do not contain an S4 tetromino.     Number [36] is a well-known problem: 9x16, 8x18, and 6x24 are also possible.  Michael Reid sent a short proof that 4x36 is impossible.

Table 4: Minimum Rectangles for other subsets

      Description             Pieces                          Rectangles
[31] Perimeter 12             BDMPpQx                           4x11  
[32] Perimeter 14             ACFfGHIJKLmNnRSTtUuVWwXYyZz     6x27, 9x18       Walter Stead
[33] Octagons                 BDMNnpQTtUuYyZz               5x18, 6x15, 9x10  
[34] Decagons                 CFfGHJRSWx                        7x9   
[35] Dodecagons               AKmwX                             6x7   
[36] equal (3-3)              ABFGIJKLmNnOPpQStUuVWYZz         12x12 etc.  
[37] symmetric                AIMOpTUXxY                        4x15           David Bird 
[38] rotational               DKmNZ                             5x8   
[39] symmetric or rotational  ADIKMOmNpTUXxyZ                 6x15, 9x10       George Sicherman     
[40] single path              GILmNnSUuVWZz                     6x13           Walter Stead [FCR June 1956, number 10,451]
[41] S1 second derivatives    CFIKLnPpRTtUVXYyZ               4x26, 8x13  
[42] N-less                   CHILRTtUuVXYyZz               5x18, 9x10, 6x15   Michael Reid

Finding minimum rectangles is only one problem that can be solved with subsets.  Other shapes can be made with some or all of the pieces in a subset.  Try making triplications with subsets having ten or more pieces, or quadruplications with subsets having seventeen or more pieces. 

Stewart Coffin's Cornucopia Puzzle is a clever idea built on the idea of hexomino subsets.  It consists of a set of 10 pieces selected from the 17 hexominoes with no symmetry which do not contain a 2x2 square (i.e. CFfGHJLnRStuVWwyz).  Each set of 10 is used to solve an 8x8 square with four holes in rotational symmetry in at least one position, and three of the usual rectangles (4x15, 5x12, and 6x10) solvable with pentominoes.   [The full set of 17 pieces can also form a 17x6 rectangle.]   100 one-of-a-kind Cornucopia puzzles made in wood were sold in 1985; each had a unique set of pieces.   Cornucopia is described in more detail in two of the sources listed in the bibliography (Coffin and Dewdney).

Superset puzzles

We've already seen that many subsets of the hexominoes can form perfect rectangles.   Perfect rectangles can also be made in various ways by adding pieces to the set.   Wade E. Philpott's article in the Journal of Recreational Mathematics (10:1) lists two: add (or subtract as seen above) an odd number of unequal hexominoes, or use a double set of 70 hexominoes.   Richard Laatsch's later article (JRM 13:1) gives a third: add two trominoes (producing an effect somewhat similar to adding one unequal hexomino).  Rectangles of 4x54, 6x36, 8x27, 9x24, and 12x18 are possible with the set of hexominoes plus trominoes: 3x72 is not.  Of these, I think 8x27 has a certain numerical elegance: 216 is the cube of 6, and 8x27 divides it into the product of two cubes. 

In addition to the trominoes, other lower order polyomino sets can be added to the hexominoes to make a set which can be made into a rectangle.  For example, hexominoes plus pentominoes make a 47 piece set covering 270 squares: this makes a number of different rectangles shown in the table below.   (This was first done in Fairy Chess Review by H.D. Benjamin and others).   In fact, every combination of the three lower order sets added to the hexominoes makes at least one rectangle.  I have added one additional group, consisting of all of the lower order polyominoes, including the single monomino and domino.  This is in the spirit of Hans Havermann's 5x211 problem using the seven lower orders.  (It is possible to solve Havermann's problem by making a 5x153 rectangle made of orders 7, 3, 2, and 1 to the 5x58 rectangle made of orders 6, 5, and 4). 

Table 5: Rectangles made by combining complete sets of hexominoes with complete polyomino sets of other orders

   Orders       Pieces  Total area   Rectangles possible
[43] 6 5          47     270         5x54, 6x45, 9x30, 10x27, 15x18
[44] 6 4          40     230         5x46, 10x23
[45] 6 3          37     216         4x54, 6x36, 8x27, 9x24, 12x18
[46] 6 5 4        52     290         5x58, 10x29
[47] 6 5 3        49     276         4x69, 6x46, 12x23
[48] 6 4 3        42     236         4x59
[49] 6 5 4 3      54     296         4x74, 8x37
[50] 6 5 4 3 2 1  56     299         13x23


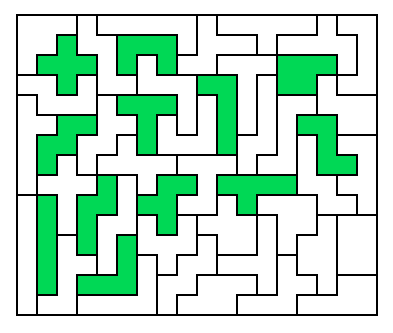
[43] 15x18 Hexomino Rectangle with Enclosed Pentomino Holes


One-Sided Hexominoes

Still another alteration to the hexominoes which makes rectangles possible is the rotational or one-sided hexominoes [51].  In this set, each hexomino without bilateral symmetry is replaced by two mirror images, which can be rotated but not turned over.  To construct such a set, glue two large sheets of paper or cardboard of different colors (say red and white) together to make a sheet with one side red and the other side white.  Cut out one full set of hexominoes with the red side face up, and another set, using an identical pattern, with the red side face down.  Now put aside one copy of each bilaterally symmetric hexomino (AIMOpTUXxY).  Don't throw them away, as they can be used for double set problems.  You will have 60 pieces left.  You must use each piece with the red side face up.  David Klarner discusses the one-sided pentominoes (18 pieces) in an anthology he edited, The Mathematical Gardner.  Solomon Golomb posed a problem with the one-sided pentominoes in his book Polyominoes.  I do not know whether the one-sided hexominoes have been studied before.  There are 42 equal one-sided hexominoes (6 symmetric and 18 mirror-image pairs) and 18 unequal one-sided hexominoes (4 symmetric and 7 mirror-image pairs).   This eliminates parity problems, so a number of rectangles are possible.  A 3x120 rectangle is impossible, as many pieces cannot be placed into a strip three units wide (they divide the strip into two groups of squares not multiples of six).  A 4x90 rectangle is also impossible, as the border is too long to be constructed from the pieces available.  The remaining rectangles are possible (18x20, 15x24, 12x30, 10x36, 9x40, 8x45, 6x60, 5x72).  This set is more challenging than the double set, because of the constraint of mirror image pairs. 


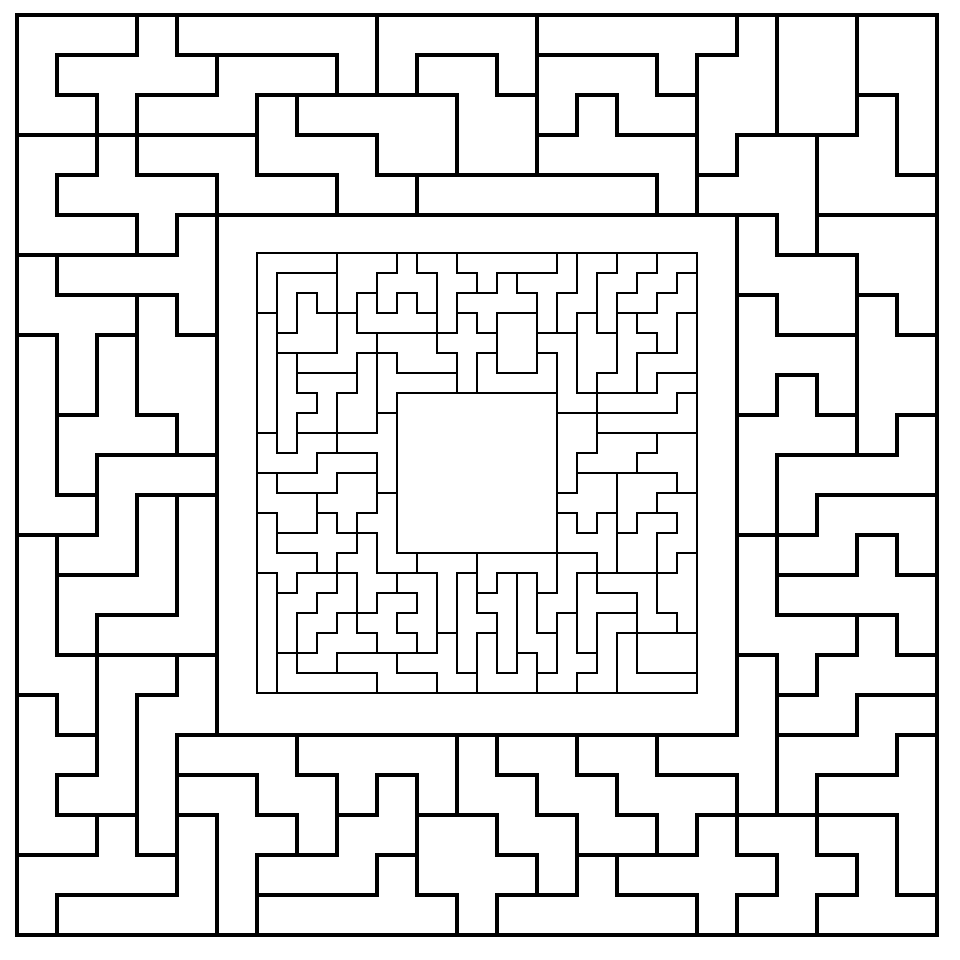
Square Doughnuts

Another shape which I like even better than the rectangle is a square with a smaller square removed.  This resembles a large square doughnut [52].   Above is part of the original cover of WGR6, showing doughnuts made with a one-sided set (large) and a double set (small).  The one-sided set doughnut is 23^2-13^2 ; the double set doughnut is 22^2-8^2 .  Doughnuts 21^2-9^2  and 19^2-1^2 (not much of a hole!) are also possible with a one-sided set; 26^2-16^2 is also possible with a double set (Frans Hansson sent out a Christmas card in 1953 with a completely symmetric solution, with only the two I's and U's shared between the two halves).   [Hansson also made a symmetric construction, 38^2-28^2, with a checkered set of 110 pieces (each asymmetric piece has four versions, each reflection having two opposite checkering patterns): this can be seen in Chessics 2:28 (see Bibliography).]

In addition to simply solving various rectangles and doughnuts with one-sided or double sets, you can try connecting as many pairs as possible [53].  The large doughnut above has nine pairs of mirror image pieces (BfJKmNuWz) connected along at least one edge (if you are using a double set, the pairs of identical pieces need not be mirror images, though it is perhaps more elegant to do so).  Another problem to try with a double set is to divide the area to be solved into two sections (equal in area but not necessarily in shape) and solve each section with one full set [54].  This was done with the small doughnut; can you divide it into two pieces so that each piece contains 35 different hexominoes?  (See the Solutions section)

Pairing pieces suggests another problem I call the Nebula Problem [55].  Use a double set to form a figure in which all 35 pairs of identical pieces are connected (asymmetric pieces must be in mirror-image pairs, but they may be oriented and connected in any way desired).  What is the smallest rectangle in which such a figure can be enclosed? My best result so far is 21x24.  I doubt a perfect rectangle such as 20x21 is possible, though George Sicherman has solved the corresponding problem for pentominoes, making a 12x10 rectangle with 12 linked pairs.


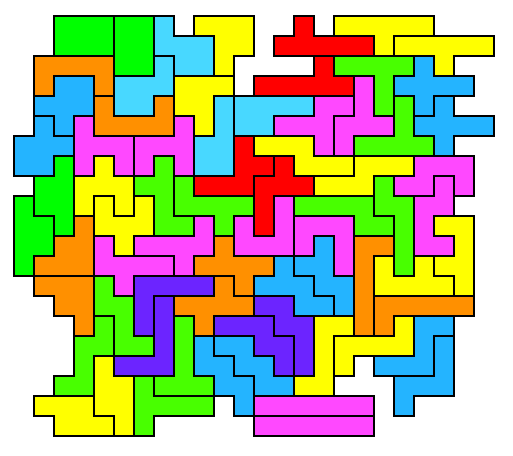
                                    Nebula

Farms


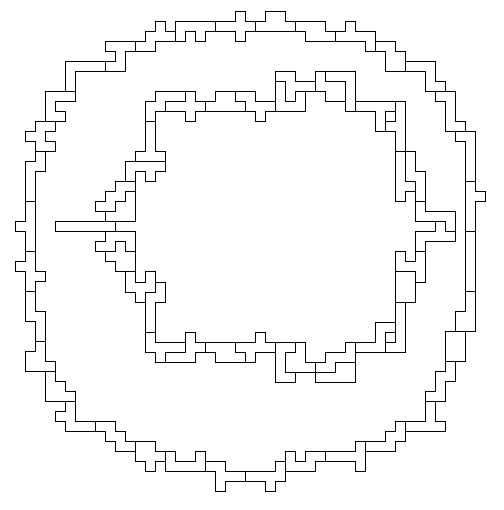
If we want to make perfect rectangles, we need more (or less) than the full set of 35 hexominoes. But there are other things we can do. Many pentomino puzzles involve farms: unbroken enclosures around an area, often of some particular size or shape.  We can do the same with hexominoes.   With an unrestricted shape, I enclosed 1578 units with an asymmetric (roughly circular) shape.   Teun Spaans and Rodolfo Kurchan observed that this could be improved to 1584 by rotating three pieces (CHP) 180 degrees.   I enclosed 584 units with a bilaterally symmetric figure (which barely fits inside the larger farm).   These are shown above at half scale.   But perfectly square farms have also been studied for both pentominoes and hexominoes:

             
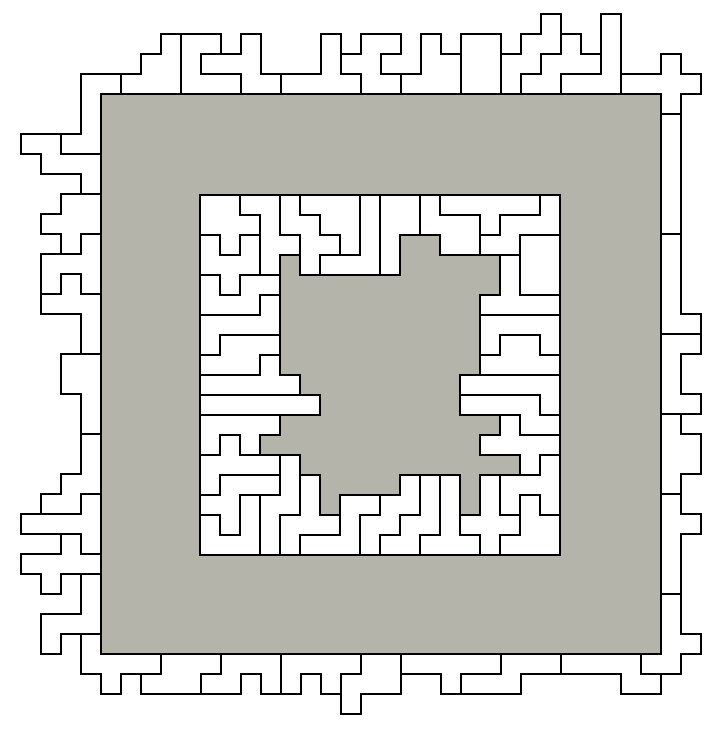
[56] Arrange the 35 hexominoes to form a square farm so that every piece touches the outside (square) border.  The farm may surround an area of any shape, though all internal squares must be connected into one whole.  The largest square possible is 29x29 (above right, outside); I believe the smallest is 18x18 (above left, inside), first discovered by Kate Jones (she wonders if 17x17 is possible; I do not think it is.)

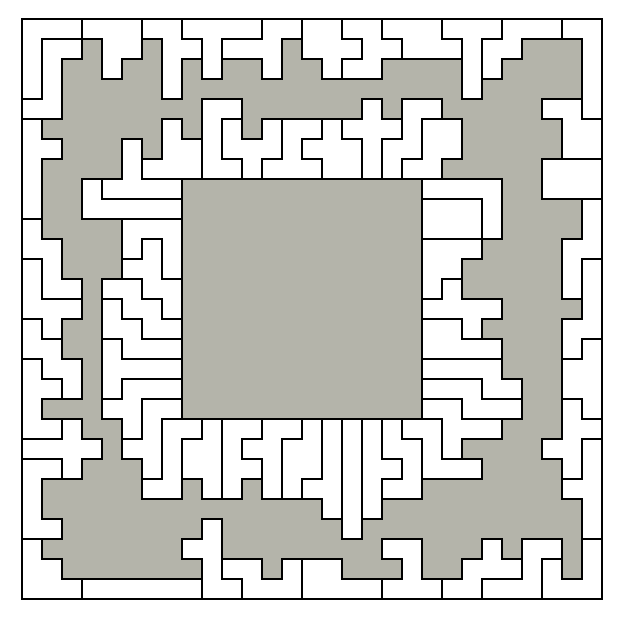
[57] Arrange the 35 hexominoes to form a farm around a square, so that every piece touches the inside square.  The outside may be of any shape, though no holes other than the internal square are allowed.  The largest square is 28x28 (above left, outside); the smallest is probably 12x12 (above right, inside). 

Internal Holes

Still another way to make rectangles with a full set of 35 is to allow internal holes. 

[58] Make a rectangle of any size with the full set of 35 hexominoes with any number of internal 1x1 holes (I call this category of internal hole problem Swiss problems, as the solutions resemble a large piece of Swiss cheese).  The holes must be solidly enclosed; they may not touch the outside of the rectangle or other holes, even corner to corner.  Holes larger than 1x1 are disallowed as well (but see Waffle problems below, beginning with [64]).  The size of the rectangle determines how many holes you need.  For example, 18 holes gives an area of 228, giving a rectangle of 12x19.   My first decent attempt was 17x14 with 28 holes; my best was 32 holes (22x11).   P. J. Torbijn  and Jean Meeus examined this problem in the Journal of Recreational Mathematics (see Bibliography).  They proved that the maximum number of holes possible in a rectangle is 50, though they were unable to construct a rectangle with 50 holes.   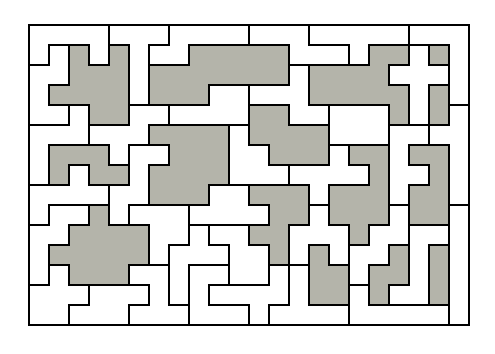Patrick Hamlyn later managed to find a 13x10 rectangle with 50 holes (reproduced from Andrew Clarke's Polyomino Pages, below left).   Rodolfo Marcelo Kurchan constructed a rectangle with 42 holes arranged symmetrically (Puzzle Fun 23, Problem 264, page 3).

                   
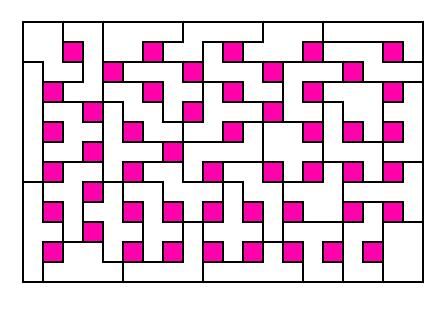
     50 internal 1x1 holes (Patrick Hamlyn)                      

Instead of 1x1 holes, use tromino holes, either straight [59] or right-angled [60].  [Mixing them is possible too].  Again, the holes may not touch the outside or each other, even at corners.  My best efforts were 10 right trominoes (15x16) and 14 straight trominoes (18x14).      Rodolfo Marcelo Kurchan improved both: Puzzle Fun 23 shows a remarkable 18x15 rectangle with 20 straight trominoes arranged symmetrically (problem 272, page 4).  Problem 275 shows 22 right trominoes.

If the outer shape need not be rectangular, a larger number of holes is possible.  Below is a 52-hole solution, by Dominique Mallet (from Andrew Clarke's pages again).   This may not be the maximum:



[61] What about domino holes?  We cannot make a rectangle with the full set of 35 (the same parity problem exists), but it makes a good problem anyway.  Discard one unequal hexomino, and enclose as many dominoes as possible with the remaining 34.   My best is 15 dominoes (18x13).   With any outer shape, my best is 35 dominoes, which appeared on the back cover of WGR11.  Rodolfo Marcel Kurchan constructed a figure with 28 domino holes (Puzzle Fun 23, problem 266, page 4) , with both the outer shape and the interior holes symmetric.

[62] Next try one hole each of progressively increasing sizes (any shape): one monomino, one domino, one tromino, etc.  As usual the holes may not touch each other.  I managed 12 holes of sizes 1 through 12 in a 16x18 rectangle; Michael Reid improved this to 15 holes in a 15x22 rectangle (see Appendix).   15 is almost certainly the maximum: 16 would be an impossible 2x173 rectangle, and there does not appear to be enough resources to surround two more large areas of 16 and 17 in an 11x33 rectangle.

[63] Make a 15x16 rectangle containing four square holes of different sizes: 1x1, 2x2, 3x3, and 4x4.   My original solution is shown below.   Later I made an expanded version with square holes up to 7x7, in a 25x14 rectangle.   This eventually became the full-color logo for Puzzle Laboratory (see the beginning of this booklet).    


Waffle Problems

Internal square holes can also be arranged in a regular grid, dropping the requirement that the outer shape be rectangular.  Every piece must touch at least one hole along at least one edge.  I call this The Waffle Problem, since the solution looks like a big (though irregular) waffle.  My best effort with 1x1 holes [64], 33 holes, is shown below.  The 1x1 holes can also be separated by two thicknesses [65], or the holes can be 2x2, separated by either one thickness [66] or two [67] (see examples below).  I managed 21 1x1 holes with a separation of two, 17 2x2 holes with a separation of one and 14 holes with a separation of two.   [In their JRM article, Torbijn and Meeus show a square Waffle, a 15x15 square with the holes arranged in a perfect 3x5 array.]

                     

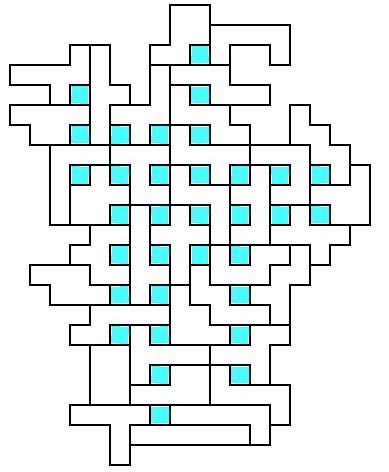
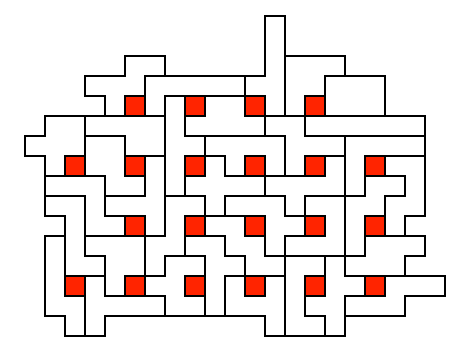
                  The Waffle Problem                                       [65]  1x1 hole pattern          
        [64]  33 holes on a regular grid                               separation 2 (21 holes)      

            
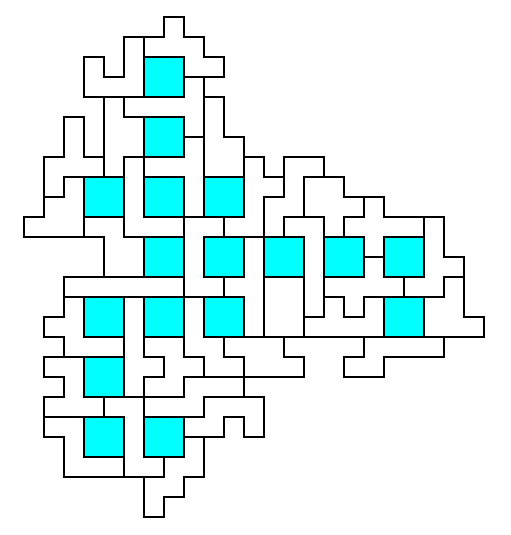
                                                                  2x2 hole patterns
       [66]  separation 1 (17 holes)                                                                     [67] separation 2 (14 holes)


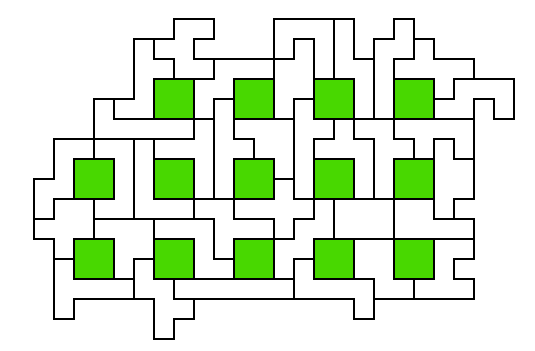
Full set puzzles: Tabbed Rectangles
    
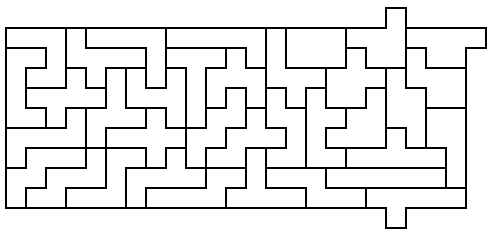
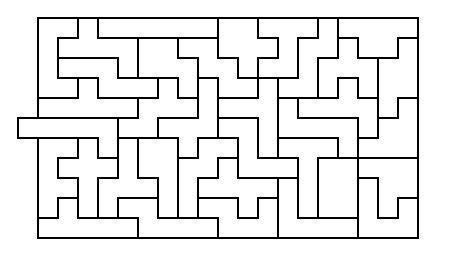
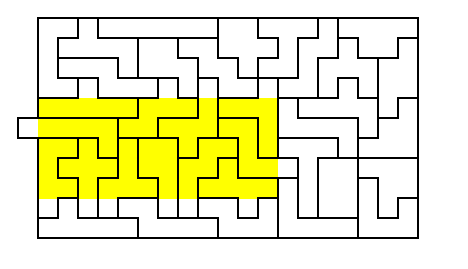
          9x23 rectangle with 3 tabs [70]                                     11x19 rectangle with 1 tab [68]
                                                                                                                                             (What's unusual about this solution?)

Instead of adding internal holes to create rectangles greater than 210 units in area, we can also form rectangles less than 210 units in area, with extra squares on the outside (called tabs).  The Japanese puzzle manufacturer Tenyo puts out a hexomino set, in its series Beat The Computer, in the form of an 11x19 rectangle with a single extra square in the middle of the long side.  There are 7 other locations [68] for a single tab on an 11x19 rectangle.  More than one tab can also be used; for example, a rectangle 4x52 with two tabs can be formed.  Do not make tabs more than one square in size or place them adjacent to other tabs.  An example of a three tab rectangle (9x23) and a one tab rectangle are shown above (the 11x19 solution shown has an interesting feature: can you spot it?).  Some of the possible tabbed rectangles which can be made are:

Table 6: Tabbed rectangles made by adding external squares

    Number of Tabs  Area of main rectangle   Rectangles possible
[68]    1              209                   11x19 (8 tab locations)
[69]    2              208                   4x52, 8x26, 13x16
[70]    3              207                   9x23
[71]    5              205                   5x41
[72]    6              204                   4x51, 6x34, 12x17
[73]    7              203                   7x29
[74]    10             200                   4x50, 5x40, 8x25, 10x20
[75]    12             198                   3x66, 6x33, 9x22, 11x18
[76]    14             196                   14x14, etc.

Is 3x66 the best tabbed 3xn rectangle possible?

The Congruent Shapes (Layer) Problem
                      
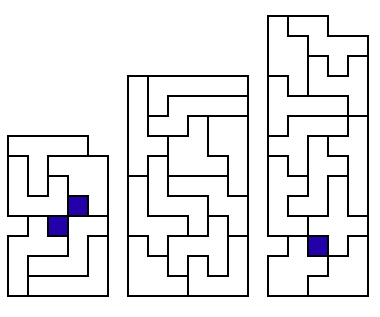
It is well known that a 3x4 square can only be made in three ways with the 35 hexominoes: Bu, OV, and pU.  But what if we use a different shape with an area of 12 squares? What figure can be solved the most ways using distinct pieces? I like to call this the Layer Problem, because the solutions to a given figure can be stacked one on top of another to make a three-dimensional figure.  The best solution I have found for 2-piece figures is seven simultaneous layers, shown below.  The table lists the best known solutions for other numbers of pieces; except for two and three pieces, all numbers of solutions are known to be the best possible.  For the larger numbers of pieces, irregular shapes are more interesting to solve. 

{In the original supplement, we wrongly stated that parity prevents 5x7 and 7x5.  It does not, but it is necessary for each layer to contain an odd number of unequal hexominoes: e.g. 3+3+3+1+1 or 3+3+1+1+1+1+1.}

Table 7: Maximum solutions to the Layer problem

                    [77] [78] [79]  [80] [81] [82] [83] [84] [85]  [86]
Number of Pieces      2    3    4     5    6    7    8    9   10    11
Maximum Layers        7   10    8     7    5    5    4    3    3     3

        
                                                          7 layers of 2 pieces [77]                                                                                          

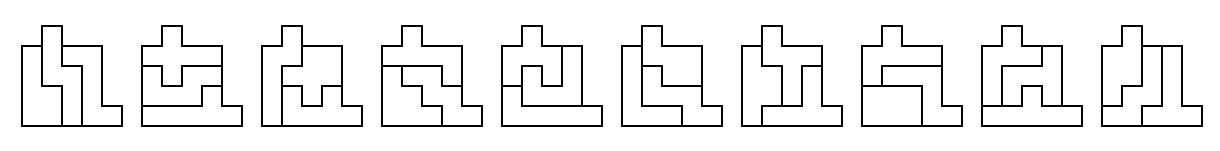
                       10 layers of 3 pieces [78]: first published on the cover of WGR11


                                                              7 layers of 5 pieces [80]


                                                                     5 layers of 7 pieces [82]


Ornamental and Geometric Figures

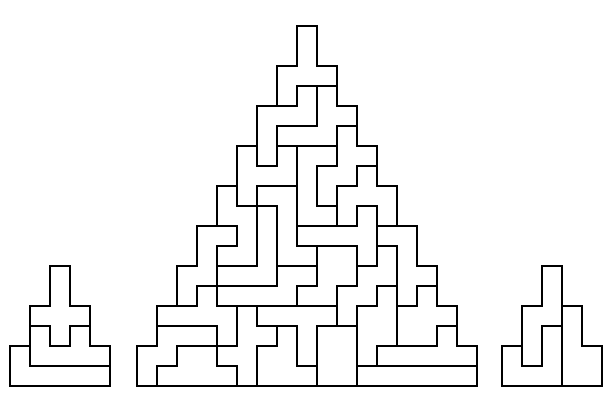
   Except for [87], which uses only 33 pieces, all of the figures below use the full set of 35 hexominoes.  [89] is a well-known problem.  Len Gordon's solution, with 1024 variants, is shown in the Appendix.

          


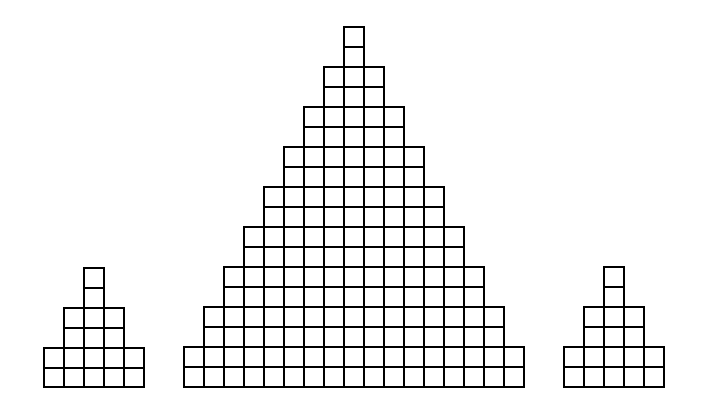
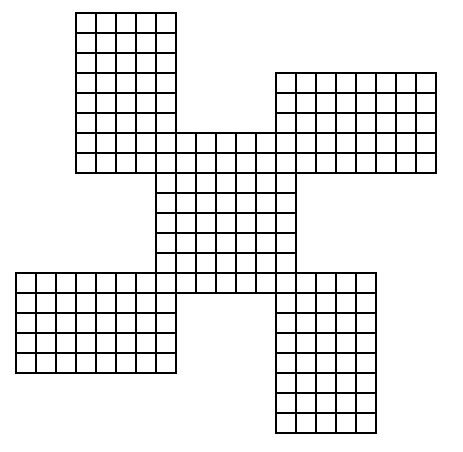
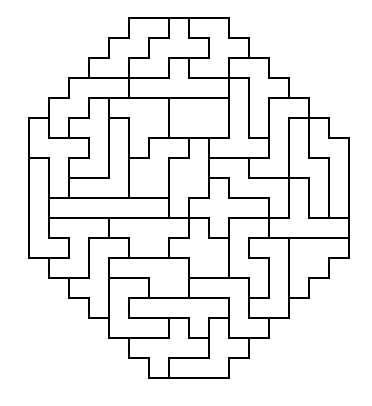
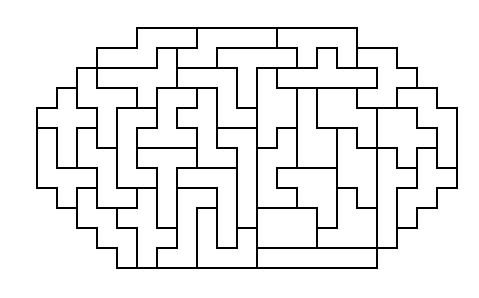
                                [87] Christmas Tree Triptych {33}                                                                [88] Windmill         



      
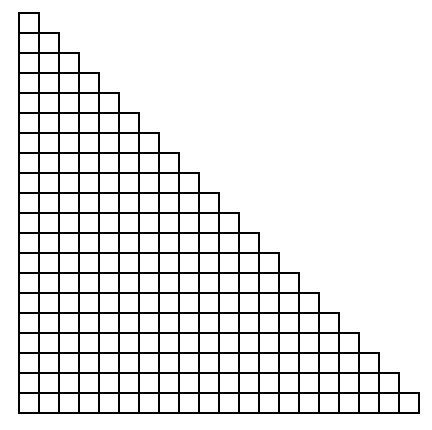
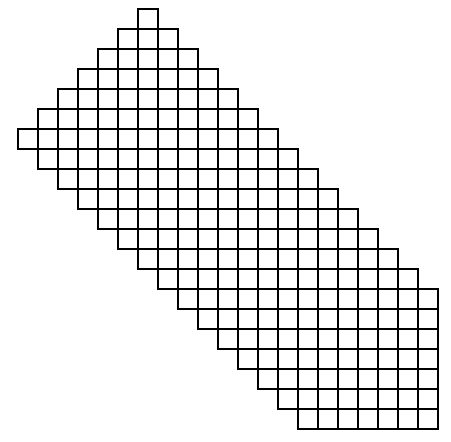
          [89] Isosceles Right Triangle                                                           [90] Pentagon

                
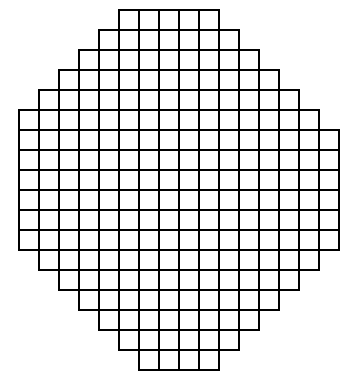
                   [91] Octagon                                                            [92] Oval               


    
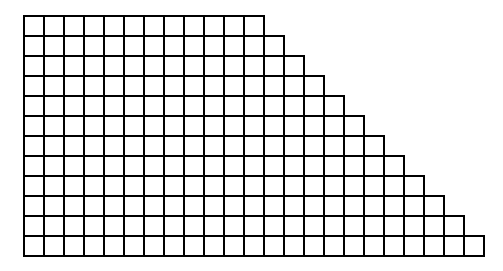
                         [93] Trapezoid                                                                              [94] Hexagon


Layer Multiplication Problems

Inspired by a construction sent to me by Teun Spaans, here are some additional problems, which first appeared in the polyform omnibus issue WGR9 in December 1989.   They all involve making multiple layers of a two- or three-piece shape, then duplicating or triplicating the figure (or both) using most of the remaining pieces.


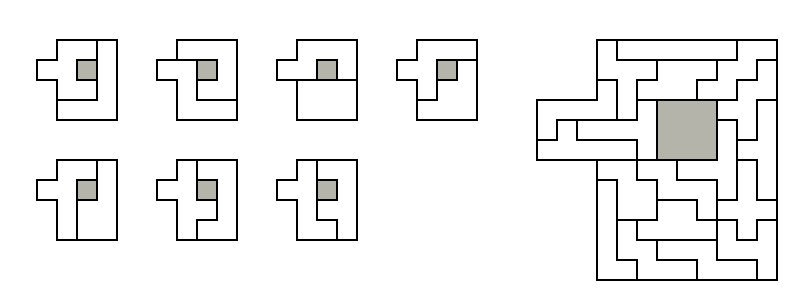
[95] Triplicated two-piece layers [32 pieces]: Seven identical two-piece layers are triplicated using all but three of the remaining pieces.   [I don't know if eight layers of two pieces are possible: if so, it may still be possible to triplicate the figure.]



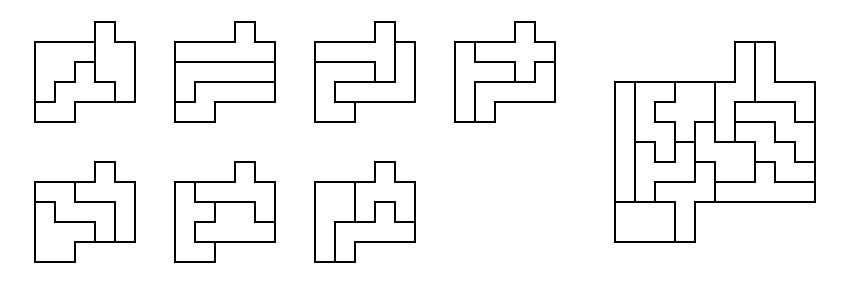
[96] Duplicated three-piece layers [33 pieces]: Seven identical three-piece layers are duplicated using all but two of the remaining pieces.


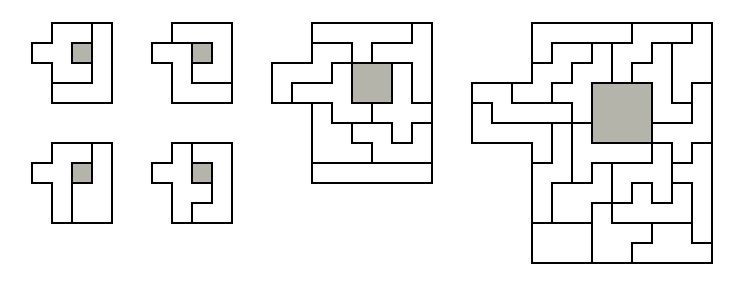
[97] Duplicated and triplicated two-piece layers [34 pieces]: Four identical two-piece layers are both duplicated and triplicated.


Full Set Multiplications

[98] One-Three-Five (first solved in 1946 by Frans Hansson): Choose any unequal hexomino and use 9 other hexominoes to triplicate it, then use the remaining 25 to quintuplicate it.  This has the advantage of being more challenging than problems [5] through [10],  but the disadvantage of having only 11 variations, since checkerboarding rules out the use of a 3-3 hexomino as the single piece.  Still, it ranks among the most elegant full-set problems.  All eleven problems are possible; here is one example:



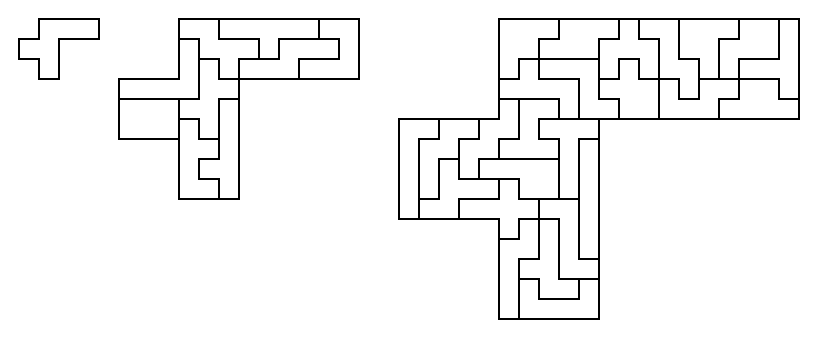
[99] The unequal hexominoes can also be multiplied in an unusual way, by converting each square to a 5x7 rectangle.  In this instance you will need to use the piece being multipled in its own replication (or you can place it in the interior and think of it as a hole the same shape as the piece being replicated).  For a more elegant solution, try to place the piece in the same orientation as the original.  This puzzle has 20 variations, as the nine asymmetric pieces produce different puzzles depending on how the 5x7 rectangle is oriented (M and x each only have one version).   Here is an example with one orientation of the w hexomino:


[100] Hexomino Solitaire (after Henri Picciotto)

In his book Pentomino Lessons (page 18), Henri Picciotto describes Pentomino Solitaire.  Two pentominoes are combined to make a figure, which is duplicated by two other pentominoes.  These two are then rearranged to form a new figure, which is duplicated by two more pieces,  etc.  The object is to form a chain (closed or open) as short as possible, containing all 12 pieces (with pieces allowed to be used more than once).   Richard I. Hess found three closed chains of length 7 (e.g. IL-TY-LZ-PV-UX-FP-WN-IL).  These all have the slight aesthetic flaw that the pieces are not always rearranged. 
     
I have tried a similar problem with hexominoes, but instead of trying to use every piece, I have tried to construct the longest open chain or closed loop without reusing a piece.  My best result is a closed loop of 15 pairs, shown below left.  I also accidentally came across two loops of only four pieces, shown in detail below right to illustrate the process used in solitaire (note that both include the pair fw).
                
                                                         15-pair loop (30 pieces)                                                                                                                                    2-pair loops


[101] Non-Symmetric Equivalences (after David Singmaster)

David Singmaster (of Rubik's Cube fame) studied pentomino figures in which the same shape can be made in two or more different ways (not counting reflections) with two, three, or four pieces. He calls these non-symmetric equivalences.  This problem was reported in Sivy Farhi's booklet Pentominoes, and David was kind enough to send me his set of solutions (2 two-piece, 18 three-piece, and 22 four-piece) found by examining solutions to pentomino problems.  In WGR7 we ran a cash contest (Contest Seven) with a $100 prize fund, asking for two-piece non-symmetric equivalences with any polyform type.   It turned out they are much more common than I suspected: Leonard Gordon sent in more than 100 and collected most of the prize fund (Anneke Treep and P.J. Torbijn also sent a few).   The diagram below shows Singmaster's two 2-piece pentomino solutions (the first is well known, as it occurs in the 2x5x6 rectangle problem), along with three hexomino figures I discovered before the contest, and another found by Gordon.  [These can be considered 1-pair loops in Polyomino Solitaire.]


       Singmaster                    Singmaster                                                                                                                                                      Gordon

[102] Butterflies

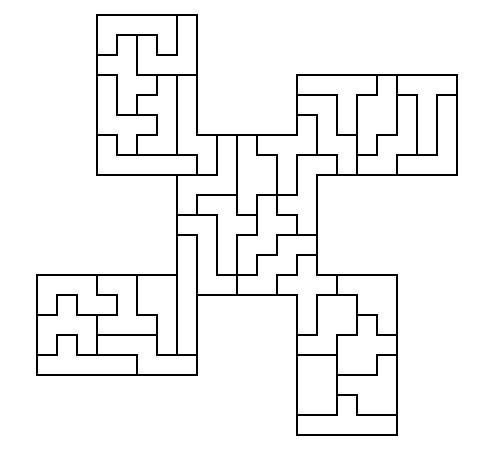
Construct simultaneous bilaterally symmetric figures of 2 through 8 pieces using the full set of 35 hexominoes.

[103] Symmetric Pairs

Construct 17 simultaneous bilaterally symmetric figures of 2 pieces with one symmetric piece left over, using the full set.



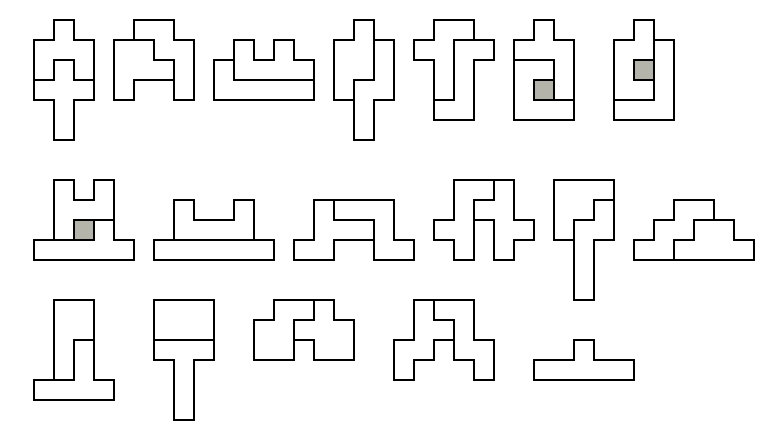
[104] Symmetric Trios

Construct 11 simultaneous bilaterally symmetric figures of 3 pieces and one symmetric figure of two pieces, using the full set.



More subsets

[105] All pieces that fit in a rectangle two units wide (CDGILNnOPpUYy) can form a 2x42 rectangle:


[106] Inflated Hexominoes

It is possible to construct rectangles (particularly perfect squares) using a mixture of polyominoes of different scales, but from the same set.   Rodolfo Marcelo Kurchan first examined this variation in 1994 in the first issue of his magazine Puzzle Fun (now available online)   He showed a number of constructions using the 12 pentominoes at different scales.   In 2017, Puzzle Fun 27 showed several hexomino constuctions by Edo Timmermans and Livio Zucca.   Puzzle Fun 36 shows a construction by Roel Huisman which is a 183750 x 183750 square using progressively larger-scaled pieces.   In the figure below left I used the first scheme by Timmermans: a 32-1-2 pattern with 32 normal sized hexominoes, 1 double-scaled piece (this must be an unequal hexomino), and two triple-scaled pieces (these must be either both equal, or [as shown below] both unequal).   This makes an 18x18 square, which seems to be the smallest possible.    The figure below right is the smallest possible rectangle, 19x12, using one doubled (unequal) piece.

  

[107] The Narrow Passage Problem

Anneke Treep posed the following problem in Ideaal, bulletin of the Math Department of the University of Twente: Using the twelve pentominoes, construct an interior hole which is no more than one unit square wide at any point (i.e. a single path of squares with no branches).   When the problem was published in The Journal of Recreational Mathematics, the best result (found by Anneke and two other solvers) was 40 units.  As originally stated, the path was allowed to touch itself at diagonals.   The Life of Games later ran a contest for the longest narrow path with hexominoes, specifying that the hole be solidly surrounded.   Aad van de Wetering won the contest with a passage of 146 units which I believe is still the record.   A number of solutions for various polyform sets appeared in WGR11 (pp. 12-13, and both covers) in June 1992.



Appendix: Additional Solutions


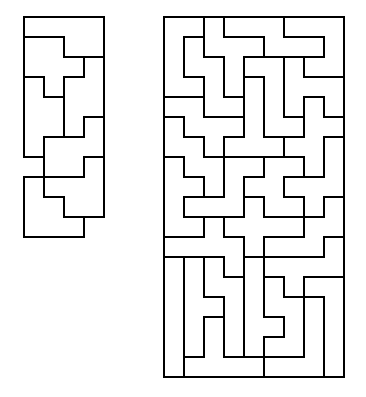
Minimal solution to [2] with five pieces


[9] Double Double Triple, using nine unequal pieces to form the base figure


[12] and [21] I-derivatives (2x13) and Z-derivatives (5x7) by Robin King


[22] Di-orthotrominoes (3x11) by George Sicherman, [37] Symmetric (4x15) by David Bird,
             and [39] Symmetric or Rotational (6x15) by George Sicherman


  
[13] L-derivatives                                               [42] N-less hexominoes
perfect 6x11 by Michael Reid                perfect 9x10 and 6x15 by Michael Reid



  [18] 5x8        [24] 6x11     [29] 5x14        
     Sergio Stanzani subset rectangles


   Perimeter 12 and 14 [31] [32]



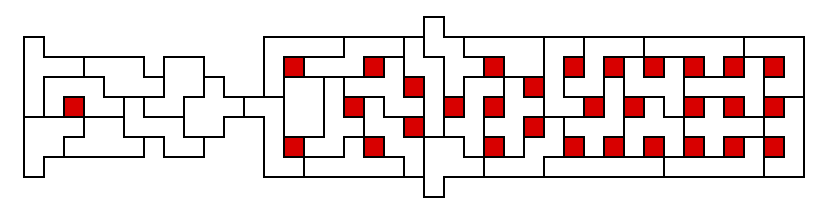
    Symmetric Swiss (31) by Teun Spaans: the pieces and holes are arranged with bilateral symmetry


     
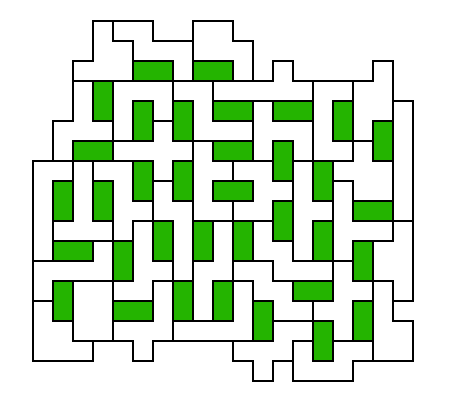
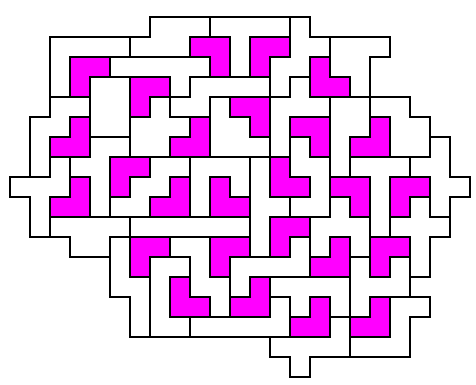
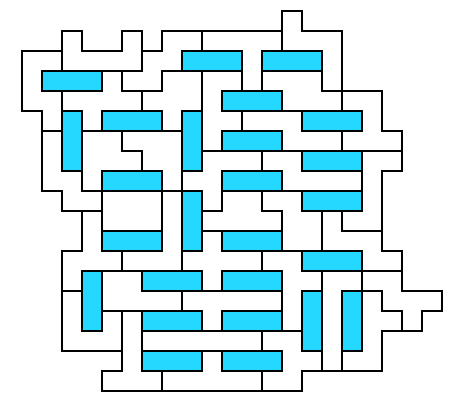
                   Swiss Dominoes (35)                                        Swiss V Trominoes (26)                                         Swiss I Trominoes (26)

     
       [52] Square Doughnut divided into 2 sets


  [62] Michael Reid's 15 progressive holes in a 15x22 rectangle



           Hidden 5x12 solution in [68]
 
          
             
                  [87] Christmas Tree Triptych                                                                    [88] Windmill                                                     
                                                                                                    


                         
                      
        [89] Isosceles Right Triangle                                                               [90] Pentagon                                                         
         Len Gordon's 1024 solutions                                        (first published on the cover of WGR13)        

Len Gordon's solution to the Isosceles Right Triangle, first published in WGR9, can be modified by reflections, rotations, and exchanges of the colored regions to produce 1024 different solutions.

            
                      [91] Octagon                                                            [92] Oval


     
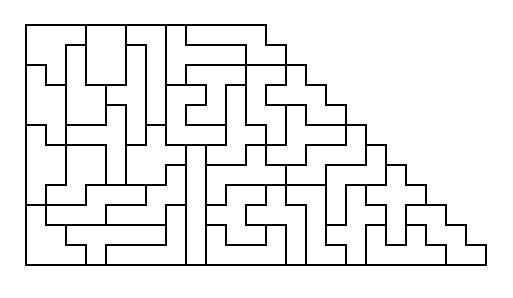
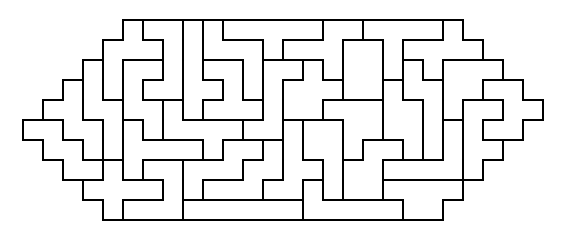
                          [93] Trapezoid                                                      [94] Hexagon


Bibliography

Far less has been written about hexominoes than their smaller cousins, pentominoes.

Hexominoes

Clarke, Andrew L., Isoperimetrical Polyominoes, Journal of Recreational Mathematics, Vol. 13, Num. 1, pp. 18-25, 1980, Baywood Publishing Co.
    (Page 58 also contains a diagram of all of the 164 polyominoes of orders one through seven, illustrating a problem by Hans Havermann: arrange them into a 5x211 rectangle.)

Coffin, Stewart, Puzzle Craft, 1985, Stewart T. Coffin, 79 Old Sudbury Road, Lincoln, MA 01773.
    More detail on the Cornucopia Puzzle.

Dewdney, A. K., Computer Recreations, Scientific American, October 1985, pp. 16-27.

Gardner, Martin, The Scientific American Book of Mathematical Puzzles and Diversions, 1959, Simon and Schuster, pp. 135-140
   Latter portion of Chapter 13, Polyominoes (originally published in Gardner's Mathematical Games column, Scientific American, 227:176-182, September 1972).
Gardner, Martin, Mathematical Magic Show, 1990, The Mathematical Association of America, pp. 183-187.
   Latter portion of Chapter 13, Polyominoes and Rectification.

Golomb, Solomon W., Polyominoes, 1965, Charles Scribner's Sons, 182pp., hardback

Havermann, Hans, N-Omino Packing, Problem 929, Journal of Recreational Mathematics, Volume 13, Number 1, 1980, pp. 57-58 (solution V.14, Num. 1, pp. 69-70)

Jelliss, G.P., Special Issue on Chessboard Dissections, Chessics, Vol. 2, Num. 28, Winter 1986
   Material on polyominoes from Fairy Chess Review (decoded by Jelliss from a special notation used in place of expensive diagrams) and the unpublished notebooks of Walter Stead.   Hexominoes are covered on pp. 144-145, and mixed sets on p. 146.

Kadon Enterprises, Sextillions, 1984, Kadon Enterprises

Laatsch, Richard G., Rectangles from Mixed Polyomino Sets, Journal of Recreational Mathematics, Volume 13, Number 3, 1981, pp. 183-187.
   Pages 185-186 discuss the set of hexominoes plus trominoes, and show a 12x18 rectangle.

Nelson, Harry L., Hexomino Packing, Problem 1064, Journal of Recreational Mathematics, Volume 14, Number 2, 1981, p. 138 (solution V.15, Num.2, p. 145)

Philpott, Wade E., Polyomino and Polyiamond Problems, Part I, Journal of Recreational Mathematics, Volume 10, Number 1, 1977-78, pp. 2-14
   Pages 12-14 show the hexominoes and give one solution to sextuplication of an unequal hexomino (C) with that piece used twice.

Torbijn, P.J., and Jean Meeus, Hexominoes in Rectangles, Journal of Recreational Mathematics, Volume 19, Number 4, 1987, pp. 254-260
   Examining the Swiss rectangle problem, proving that 50 holes is the maximum possible, though they did not manage to find a solution (later solved by Patrick Hamlyn).   They show a number of solutions, including a 15x15 square with 15 holes arranged in a symmetric 3x5 grid (as in the Waffle Problem), and a 16x16 square with 46 holes, the best-known solution until Hamlyn.

Relevant Sources on other Polyominoes

Farhi, Sivy, Pentominoes, 1981, Pentacube Puzzles

Klarner, David A., The Mathematical Gardner, 1981, Van Nostrand Reinhold

Kurchan, Rodolfo Marcelo, Puzzle Fun, 1994-present
   Primarily devoted to pentomino constructions, but constructions for hexominoes and other sets appear frequently.

Martin, George E., Polyominoes, a Guide to Puzzles and Problems in Tiling, 1991, Mathematical Association of America, 184pp., paperback, ISBN 0-88385-501-1

Treep, Anneke -- The Narrow Passage Problem, Number 1739, Journal of Recreational Mathematics, Volume 21, Number 3, 1989, page 220. [Solutions in Vol. 22, Num. 3, pp. 237-238.]



This compilation of WGR was published on January 7, 2024.   Most of the diagrams were made using a new drawing module written for Puzzle Virtuoso.  Roel Huisman submitted diagrams for his own solutions.
This article is copyright © 2024 by Michael Keller.  All rights reserved.