Icelandic Oratorios, or How I learned to play (the) Accordion

This article would not have been possible without three people in particular who got me interested and helped me learn to play Accordion: Jason Crupper, Rick Holzgrafe, and Mark Masten.

I originally learned the solitaire game Accordion from Albert Morehead and Geoffrey Mott-Smith's classic book The Complete Book of Solitaire and Patience Games.  Morehead and Mott-Smith put the odds of winning at 1:100, but explain that 1:100 is a shorthand for games where the win rate is extremely low.

The way the game is traditionally dealt is to turn up cards one by one from the stock, putting them in a row left to right.   If adjacent cards are of the same rank or suit, the one on the right (i.e. most recently dealt) can be placed on top of the one on the left (we will call this move a slide). The same can be done with cards three positions apart; the card to the right jumps over two cards and is placed on the card three positions left if it matches in suit or rank (we will call this move a leap). Piles of cards thus form, and a pile of cards is treated as a single card (following the card on top), and can be moved left or piled on from the right.  As the game is dealt, the row of cards expands (as cards are dealt from the stock when no plays are possible) and contracts (as several plays are sometimes made in succession), rather like the musical instrument which thus gives the game its name.  Like most people, I played quite a few times without success.  The game was originally known as Idle Year, because of the way you can play hundreds of games without winning.  William B. Dick (in Dick's Games of Patience, 1884) says: "This Patience is styled The Idle Year because, with a well-shuffled pack, it will require about that length of time to accomplish it."   The earliest version was completely self-working: the player could not deal a card if any plays were available, and a leap was only allowed when no slides were available.  (Walter B. Gibson describes this version in his 1964 book How To Win At Solitaire, before moving to a freer version of Accordion.)   Many years ago I wrote a very simple solver to simulate the play of Accordion, making slides whenever possible and leaps otherwise, winning 4 times in a sample of 10,000 deals (an updated version of this is described below under Traditional Play).

The first inkling I had that the game can be played a different way was when I read the strategy guide on the website for Solitaire Till Dawn, a solitaire package for the Macintosh programmed by Rick Holzgrafe. He suggested dealing the entire deck out ahead of time, turning the game from a closed solitaire into a fully open one. He also described a strategy for using sweepers (cards of the same rank which are accumulated at the back of the tableau) and winning about a third of the time. We'll get back to this strategy later on, with examples and elaborations. I didn't have access to a Macintosh when I first read the article, so I put it in the back of my mind until a number of years later.   [Of course, the open version only contracts, so the name Accordion isn't as descriptive anymore.  But the name is colorful, so we'll keep it, like floppy disks.]

The idea that the game can be won in open style spread, and dealing out the entire deck has become a common method of presentation in solitaire packages, including BVS Solitaire. I saw an online version by Andrew Pipkin, programmed in Java, in which the entire deck is dealt in one overlapped row of 52 cards. I like this way of dealing, but not the way he shows slivers of the covered cards, which makes quick visualization of moves much harder as the piles get larger late in the game, and has the disconcerting visual effect of making the selected card jump backwards when the piles are large.

Mark Masten did some computer analysis of the open version of Accordion which he reported to a solitaire mailing list in April of 1999. He played 25,000 deals by computer, and gave the astonishing fact that every single deal was solvable! It appears that open Accordion has one of the highest win rates of any open solitaire, almost certainly even higher than FreeCell. Gordon Bower calculated that it would take 270,000 wins without a loss, or less than five losses in 714,000 deals, to argue statistically that Accordion has a higher win rate than FreeCell. By 2000, Mark's solver had played around 800,000 deals without a loss! Jason Crupper showed, on the Pretty Good Solitaire forum, that impossible deals can be constructed (in fact, deals with no possible moves), but to my knowledge no random deal has ever been shown impossible. Jason first wrote to me about FreeCell (flourishes) in 2002, and we later started talking about Accordion too. He wrote a computer version using the programming language Scheme, and played many games, winning every time. He sent me a copy of his program and some examples of won deals. This is a nice version, with numbered deals, undo, and most importantly, automatic recording of wins. Jason uses a simple notation for moves which I will also use here. I finally started playing seriously, learned the basic technique described by Rick Holzgrafe, and started winning a few times. I then figured out some elaborations of his strategy, and I have now reached the point where I can win (at least eventually) 98-99% of the deals. So let's see how to play...

Basic rules of Open Accordion

The deck is dealt out as an overlapped row of 52 cards.  Cards are played right to left: a card may be moved onto the card immediately to its left, or three cards to its left, if the two cards are of the same suit or rank.  The covered card becomes part of a pile, which moves in exactly the same manner as the card at the top of the pile.  Piles are shown as single cards for clarity.   The object of the game is to reduce the cards to one pile.

Accordion Virtuoso

After playing Jason's program and others, I started to develop my own version, using a single row of cards as in Pipkin's version, but simply made covered cards disappear entirely. I also added an option to freeze a rank of cards to prevent them from being accidentally covered until near the end of the game. I incorporated Jason's solution notation, putting it in a text box on screen (this allows partial solutions to be recorded easily). I have gradually added other features, including unlimited undo, variable leap values, and other variants, as described below.

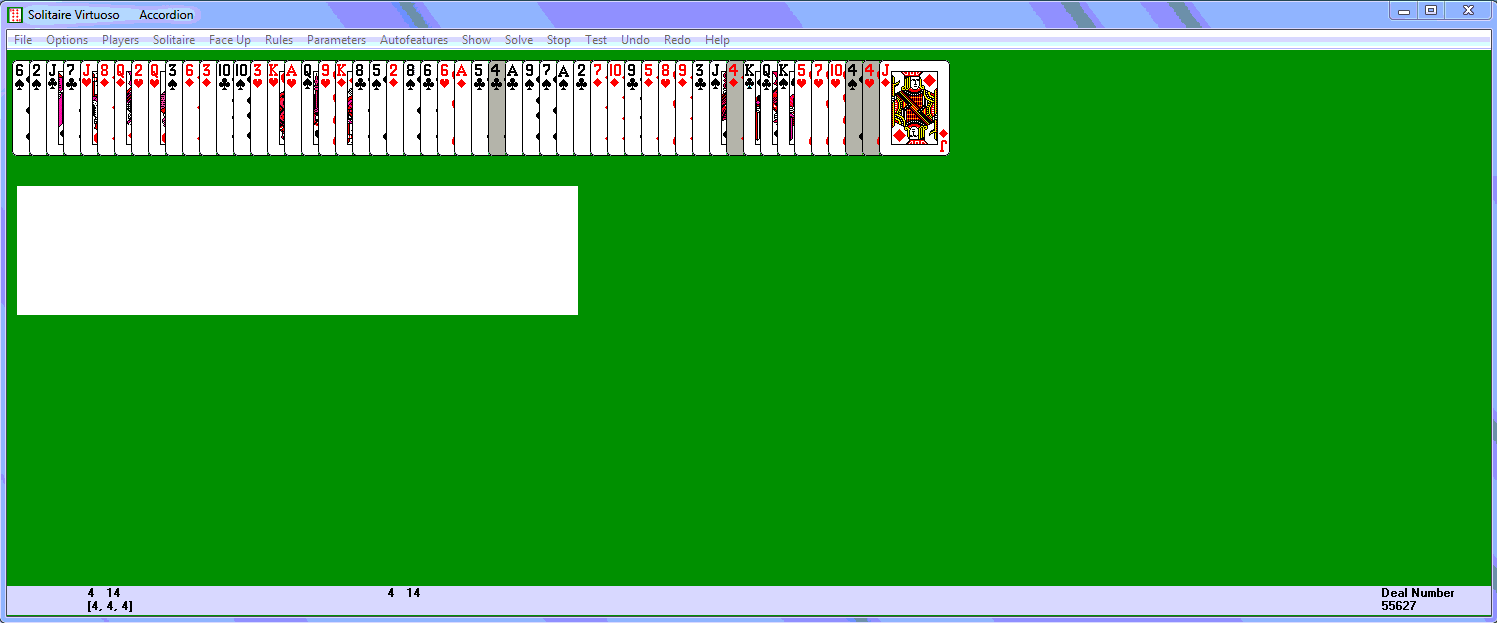
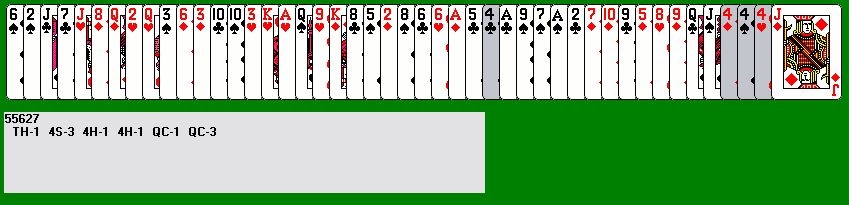
Here is a screenshot showing the Accordion game. The entire deck is fanned out from left to right. The program calculates a simple function to select the best rank to try as the sweeper rank: the best choice is shown in the lower left corner, in this case fours, which have a very low score of 14 (other ranks with low scores may be shown in the larger gray window directly below the cards; in this case the program finds no other good candidates). The program also shows which candidate is the first, counting from the right end, to have two, three, and all four of its rank appear. In this case fours appear twice, three times, and four times before every other rank.  The fours of hearts and spades are already in ideal position; there is only one diamond behind the 4D and six clubs behind the 4C (so the evaluation function for fours is 1x1x2x7 = 14).   All four cards of the best candidate rank are highlighted, and they may not be discarded normally while highlighted.   The F8 key or the Rules/Protect Rank menu will turn off the protected rank.  Clicking F8 again will turn the background dark brown; clicking on any card will then make that rank the new protected rank.  

Accordion Virtuoso works on a single click system: a left mouse click sends the card you are clicking on either one (slide) or three cards (leap) to the left (if both moves are possible, it slides). A right mouse click automatically leaps if possible, doing nothing otherwise. This takes a little practice to get used to, but you can play pretty quickly (using mostly left clicks) once you are familiar with it. If you make a mistake, the Undo option will immediately take back your previous move (any number of consecutive moves may be undone).   A text box will keep track of how many undos you have used (this is for the player's information: there is no penalty).  Highlighted cards can be moved (either slide or leap), but not discarded by normal clicks (another card cannot slide or leap onto them), which prevents you from accidentally discarding sweepers.   Highlighted cards can be discarded if you hold the Alt key down while left or right clicking.

Winning a simple deal -- basic techniques

When presented with a deal, the first thing to do is to try and find a rank where all four cards are near the end of the row of cards. Usually this does not happen, but you want to pick a rank where two or three of them are near the end and the other(s) are not too far from it. In particular you want as many of the four cards as possible to be the last card dealt of their respective suits -- or to be able to get them there quickly.   If we can get there and then bring the four sweepers together, we are in what I call ideal position.   This is not always possible; it is usually achieved at or near the end of the game, and sometimes not at all.

The first task is to get rid of the cards between the three fours, and get the jack of diamonds in position where it can jump over the fours. We start by moving the ten of hearts onto the seven of hearts, allowing the four of spades to jump over two hearts onto the king of spades, leaving those hearts open to be discarded in turn by the four of hearts. The queen of clubs covers the king of clubs, then leaps over to the three of clubs (equivalent to consecutive leaps by the king and queen of clubs). Note that we are saving the jack of spades as a target for the jack of diamonds. The program automatically displays each move made, using Jason Crupper's simple notation: the card moving is abbreviated (T for ten, etc.), followed by a dash, and a one for a slide and a three for a leap.

We want the jack of diamonds to leap onto the jack of spades, but there are too many cards in between at the moment. So we need to leap with one of the fours. The four of diamonds can do so right now; this is not a perfect move, since we want to get the jack of diamonds past the four of diamonds, but it allows us to make some progress by leaping with the jack of diamonds. Leaping next with the five of diamonds allows the queen of clubs to make a double leap, and now the jack of diamonds can get past its four, sliding one more card after that. Three of our sweepers are now together in perfect position, and we leap onto the eight of hearts immediately to their left (we generally make this kind of move whenever possible).

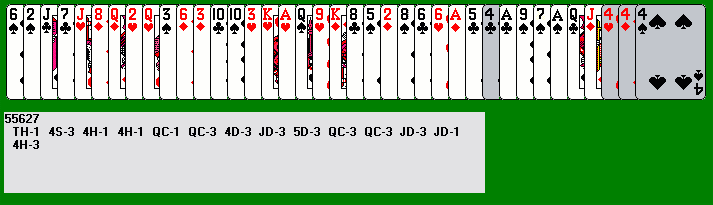
There are various ways to clear out most of the cards between the fours of hearts and clubs. We might think about keeping the ace of diamonds as a target for the jack, but the jack is already to the left of its sweeper.  It's easier to eventually leap the four of hearts and slide onto the jack.  So we choose to leap with the ace of clubs, mop up two spades with slides, then leap with the queen of clubs and ace of spades, sliding onto the queen of clubs after that. Now only the jack of diamonds remains to the right of the last four.  If we now leap with the ace of spades, then mop up the six of clubs, we can leap onto the six of hearts as we had planned. Now we mop up the jack of diamonds, and our sweepers are in ideal position (this doesn't often happen before the midpoint of a deal).

Now we push cards to the left, looking for opportunities to leap or slide onto the card immediately to the left of the cluster of sweepers. Here we leap with the two of diamonds and mop up a spade. The spade cannot be discarded right away, but if we leap onto the eight of clubs, the ace becomes close enough for the four of spades to leap onto it. We generally try to avoid breaking up the cluster unless we can immediately close it up again, but the two card maneuver we just did is a basic one -- we can do the same thing again after leaping with the nine of hearts. Another useful maneuver is a series of leaps with consecutive cards of the same suit. In this case we can leap with three hearts in a row, each landing on the previous one. Then we mop up both tens with slides.

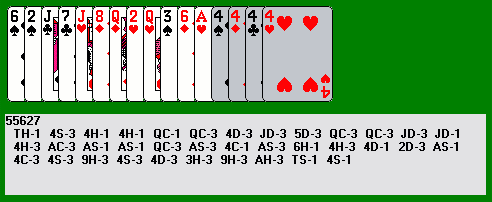
Now we do our basic maneuver, leaping with the four of diamonds before re-closing with the four of hearts and continuing with a four of spades leap. Instead of doing two leap-slide combinations with the fours of hearts and diamonds, we see that we can actually mop up the other four red cards with the queen of hearts if we eliminate the eight of diamonds with a slide first. Now we leap into the queen of hearts, and see that we have only four cards left besides the sweepers. Since we have no other red cards left...

...we could unhighlight the sweepers and eliminate the two red fours, but it's easy enough to finish with all four sweepers alone (I naturally call this an ideal finish). If we slide with the seven of clubs, the four of spades has room to leap and slide, followed by the four of clubs. Now we unhighlight the sweepers...

and a series of slides produces a win.  (You can hold down the Alt key instead of unhighlighting sweepers).  The background turns orange to signal a win, and there is a trumpet fanfare (usually a cascade of cards will occur too, but we turned it off to allow a clear screenshot of the final position).

Trailers

Sometimes the last card in the row is very difficult to get past the sweepers. I figured out that you can leave one card behind the sweepers, and finish by placing this card on top of the sweeper of the same suit.

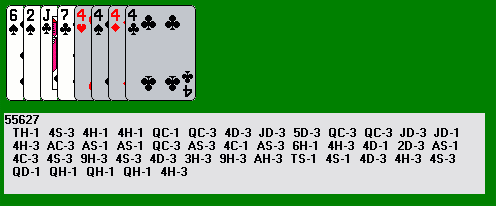
The deal shown above is number 57988. The program recommends tens as the best sweeper (sevens are a distant second). In order to start clearing the cards amongst the first three tens, we leap with the jack of hearts, setting up several other plays which reduce the cards before the ten of clubs down to three. No other plays are available towards the end of the row, so we go down to the nine of clubs, which is in the middle of a string of cards of two alternating suits. These are hard to break up unless we can pull one of the cards out -- in this case we leap with the nine of clubs, opening up other moves. Later we reach the following position; the four sweepers are together; our plan is to eliminate everything else, finishing by mopping up the other three tens with the ten of hearts, and covering it with the seven:

Suit reduction

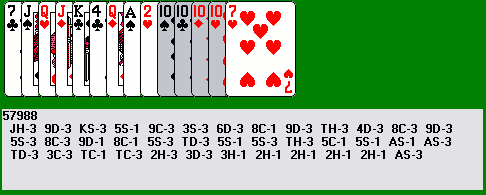
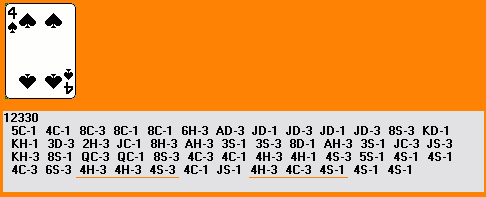
Sometimes three of the same rank are in ideal position, or nearly so, but the fourth is at or near the beginning of the row (particularly when it is the first card of its suit dealt). You can still win these deals by carefully discarding all but one of the cards of the problem suit (except for the sweeper rank) and eliminating the last non-sweeper of that suit by covering it with a card of the same rank. Here's a good example, deal number 12330:

After three moves, we have the first three sweepers together, and start to reduce the diamonds in the middle of the row by a series of leaps and slides:

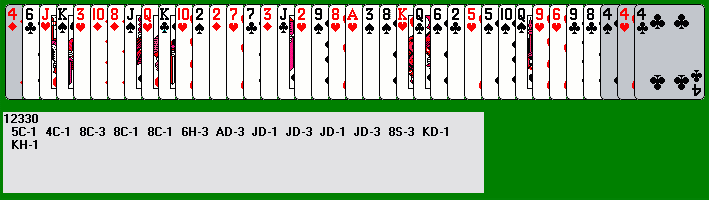
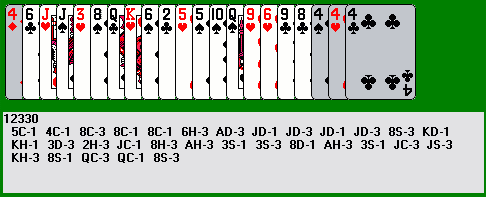
Now we get rid of the two and three of diamonds using the three of spades, and the ten and eight of diamonds using the eight of spades, leaving us with only the four of diamonds at the far left. Using the other three sweepers, it is easy to mop up the cards of the three remaining suits. Note that twice we leap with the four of hearts (the second time onto the four of diamonds, after unprotecting the sweepers with the F8 key) to set up an ABBA pattern of suits which we eliminate with a leap and a slide. This is a very basic technique (underlined in orange, below right):

Flotsam

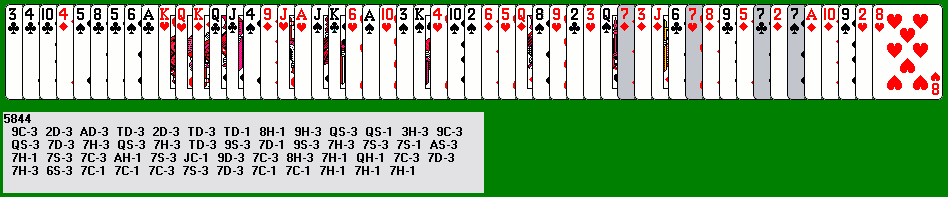
Sometimes all four of the same rank are in the first dozen or so cards, but there are a number of cards (I call them flotsam) at the end of the row behind the potential sweepers. If you can condense these cards and gradually get them past the sweepers, you can still win.  Here's deal number 5844, fully played out:

Pretreatment

Another technique sometimes needed in hard deals I call endgame pretreatment. Sometimes you reach the last few cards of a solution and hit an impasse, when there are no plays left. Above is an example, number 63351, the first time I used a version of this technique. Notice how the last few cards have several alternations in suit (the hearts and diamonds alternating from the third through sixth cards) and rank (tens two apart at the far left).

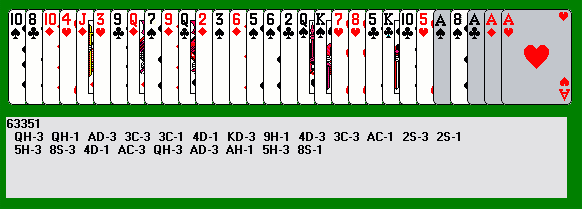
After reaching the point shown above, I was getting stuck if I tried going forward in the usual way, so I tried a different approach, making a series of plays at the left end. Gradually the endgame untangled, and I was able to win:

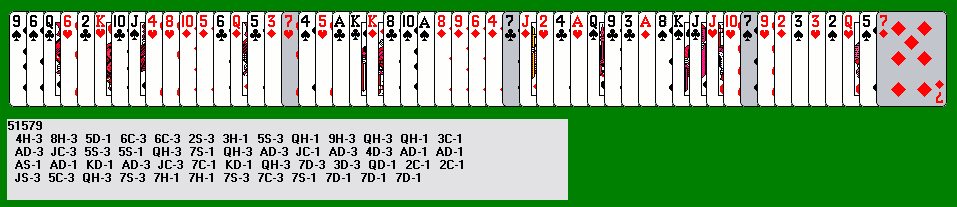
After winning that deal, I started to look for chances to use this technique, when a deal was proving hard to solve. I started using it at the very beginning of a deal (hence the name pretreatment, as in doing laundry) when I could see that the lefthand end was giving me problems. Here's another example, 51579, where I made a series of five pretreatment plays at the very beginning of the deal (see how the six of clubs gets inserted in to break up the nasty alternation of clubs and hearts). AV liked threes as sweepers, but I got nowhere until I switched to sevens, eventually winding up with an ideal finish:

I have now played over 600 deals with Jason Crupper's Scheme program and more than 4000 with Accordion Virtuoso, and have less than 30 AV deals I have so far not been able to solve.  I suspect that a small frection of deals, less than 1 percent, are not solvable with the sweeper technique.   The hardest deals I have solved in Virtuoso are 6777, 11717, 13506, 15723, 33135, 47593, 50653, 59532, 62185, 72685, and 85055.  But the hardest deal I have solved yet is number 101862164 in Jason's program, here imported into AV:

Accordion's Revenge

Mark Masten later thought up and tested a harder version, which he called Accordion's Revenge. A card is selected from the 52 cards dealt, and the game has to be won with the selected card at the top of the pile at the end. This is impossible with the first two cards dealt, but can be done with any card from the third to the last. In fact, he ran 500 deals with each of the 50 possible positions, and still won every single deal!

This can be played in Accordion Virtuoso by clicking the Rules/Revenge option after choosing Accordion as the game.  This will pick a valid AR card at random from the 50 possible choices.  If you turn off the Rules/Random Revenge flag, the program will put up the Card Tracker to allow you to choose your own card to finish with: click on File/Choose Deal (the current deal will be preselected; click OK, then click on the card you want in the Card Tracker). While I was learning to play, I also practiced winning some deals while finishing up with the third card dealt. This may be the hardest position on average to win with. Let's see an example of how this works:

This is deal number 7795. The seven of hearts, shown jogged upward, is the card we want to finish with on top. The general approach is to get the sweepers down close to positions 4, 5, 6, and 7. We eventually want to get either all four sweepers in turn to position 1, finishing with the four of diamonds, or the four of hearts to position 2 and the last sweeper (of any other suit) to position 1. The position below left shows most of the deal played out, with the sweepers ready to make the last few moves. The four of diamonds leaps onto the seven, the four of spades onto the queen, the four of hearts onto the four of diamonds, the four of clubs slides and then leaps, and two slides finish the deal (below right).

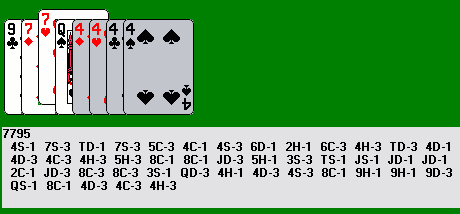
The finishing card (AR card for short) can occur anywhere except for the first two positions. There are at least three basic strategies for winning at Accordion's Revenge, depending on the position and rank of the AR card. If the rank of the AR card is a reasonable sweeper candidate, it is usually easiest to choose that as the protected rank, bring the sweepers together with the AR card last, and finish as usual. Otherwise, the AR card will eventually have to be a trailer: if the AR card appears far to the left, the most sensible approach is similar to deal 7795 above: push the sweepers down to the AR card, then try to leap over it and sweep up the remainder of the cards left of the AR card, then consolidate the sweepers down to one of the same suit as the AR card. If the AR card is far to the right, it will probably be easiest to maneuver any sweepers and flotsam around it, then play an ordinary sweeper strategy. Here's another example. Notice the last few plays, where the queen mops up the last sweeper and a couple of other cards.

This mopup technique is seen quite often when....

Playing with bigger leaps

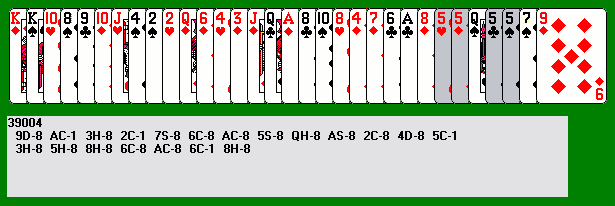
Andrew Pipkin's Java version of Accordion had options to allow any combination of slides and leaps from 1 to 6 cards. He added these to make the game easier, under the common misunderstanding that the standard 1/3 game was too hard to win. Mark Masten investigated various leap values using his solver, and discovered yet another surprising fact: many of the variant games with a one-card slide combined with a single leap value greater than 3 are quite playable and can be won fairly often; in fact the medium leap values of 4 through 6 may even be easier than the standard game. I added leap values from 2 through 10 to the Accordion Virtuoso program and began to experiment with them. I have now reached the point where I can usually win with leap values up to 7. Test runs with the solver show that most deals are winnable even up to leaps of 10. It appears that a leap value of 2 is quite difficult; the solver wins a substantial number of them (at least 40%), but its strategy seems impenetrable and I have been unable to win myself yet. Let's see how the strategy for larger leaps works. Here's deal 39004, played with a leap of 8. I chose fives as the sweeper instead of the recommended sevens:

The early moves are mostly leaps, trying to clear the flotsam from the area between the sweepers, though slides are used occasionally to line up leaps correctly.

Now we start to eliminate clubs and spades. By the time we have reached the position below, most of the clubs and spades are gone.

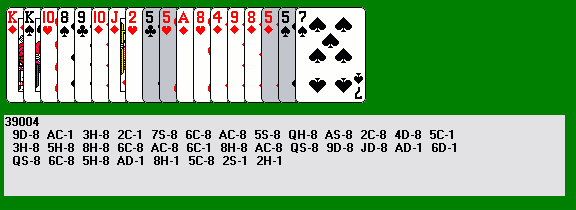
We plan to leap the nine of diamonds onto the nine of clubs (eliminating the last non-sweeper club) and the eight of diamonds onto the eight of spades. We eventually plan to leap the seven of spades onto the king of spades (after the latter has picked up the king of diamonds). The aim is to reach a position where every remaining card can be removed with a series of slides. Each sweeper picks up the remainder of its suit (or a stray card of one suit is picked up by the same rank of another suit, as the ten of diamonds does below), and the last sweeper mops up the remaining cards of its suit and all of the remaining sweepers:

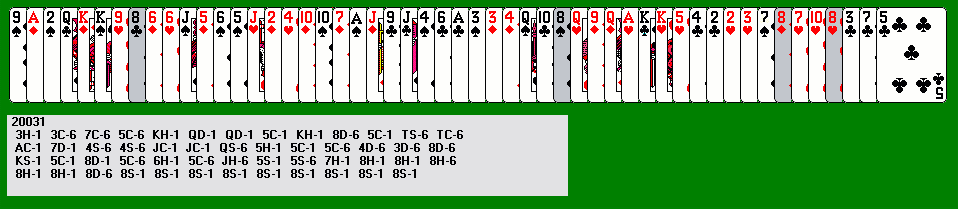
Here's one more example, with Leap-6, ending in a mopup of the last nine cards. Note also another technique of consolidating suits here, collecting several cards of the same suit in a row and using them as a sort of landing strip to leap onto with other cards of the same suit.

23 Skidoo -- Playing without Slides

A barely explored question is what happens if there are no slides, but two sizes of leap. In particular, what happens if you can leap either 2 or 3 to the right?  Obviously it is impossible to reduce to one card, but how often can you reduce to two?  I call this variant 23 Skidoo.  Here is a successful game: in Accordion Virtuoso, the Control key momentarily decreases the leap value by 1, so this can be played using only the right mouse button and the Control key (otherwise you would have to toggle constantly between leap values).  This is an unusual game which requires some different strategies: an important maneuver is reducing a pair of adjacent cards of the same suit by leaping both onto another card of the same suit.   Suit elimination is an important technique in the later stages.

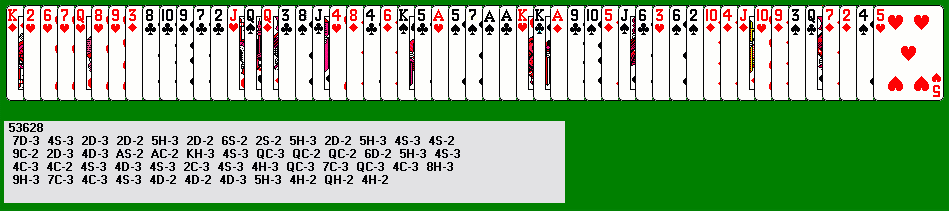
Mark Masten's solver data indicates that the 2/3 version has a very high win rate, like standard Accordion, and may in fact be easier.   It can also be played with other combinations, reducing to the same number of cards as the smaller leap value (I've reduced to three cards in 3/4 and 4 cards in 4/5).

More features of Accordion Virtuoso

Two optional help features available to the player (both are off by default, but can be switched on and off at will from the options menus) are shown below, partway through a deal. The row of colored squares directly below the card show which cards can currently be played (AutoCount). Black squares show available slides, white squares leaps, and red squares show cards able to either slide or leap (showing available leaps is particularly helpful in long-leap games). The Card Tracker at the bottom right shows which cards have been covered, making it easy to see at a glance which cards of a particular suit or rank are still left. In addition, the program automatically signals when no more moves are available by turning the background blue; this AutoEnd feature is on by default and is independent of the AutoCount option.

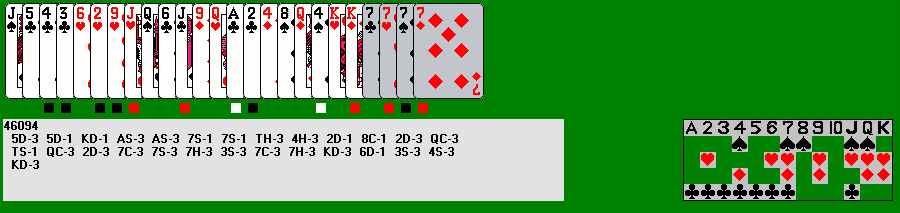
Concertina

Many years ago, before I understood Accordion very well, I came up with a variant, which I naturally called Concertina, where a card (or pile) on the right may, if desired, be placed underneath the card/pile one or three positions left; we could naturally call these moves underslides and underleaps (or more colorfully, ducks and dives).  Note that if both slide and leap are possible with the same card, underslide and underleap have the exact same effect).  [Using Concertina rules, it seems likely that Accordion's Revenge is usually winnable even if the AR card is the first or second card dealt, using it as a kind of reverse trailer.]  Since the standard game is usually winnable already with most leap values from 3 to 10, I now suggest that Concertina be played with a leap value of 2. In Accordion Virtuoso, clicks with the Shift key held down will produce an underslide or underleap; these are symbolized with plus signs instead of dash/minus signs. Here's a fully played out example:

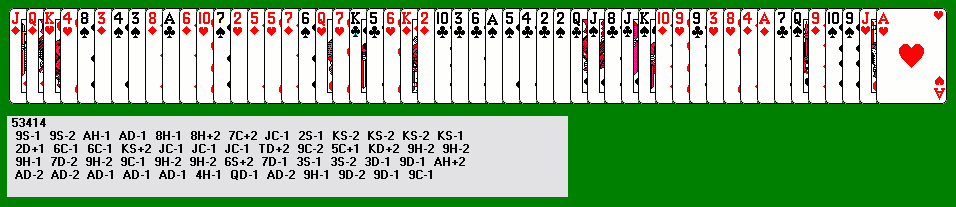
There was one online version of Accordion (now vanished) where the programmer mistakenly programmed underslides and underleaps only.   I don't know what the strategy of this variant would be, or even if it is playable/winnable.

Other variations

Mark Masten has also suggested using alternate decks, in particular a 49-card deck consisting of seven cards each of seven suits. Obviously it is possible to combine any of the above variations; in particular playing Accordion's Revenge with larger leap values makes a very challenging game.

Another idea, which I have only tried in a couple of hand-dealt games, is to play a two-dimensional version with four rows of 13 cards (this needs some space; overlapping the cards in the normal fashion is awkward).   Horizontal plays in rows are as usual; vertical plays may be made in any direction and at any distance.   A row contracts automatically when a card from it moves upward or downward into another row.

Smaller versions

Accordion, like many solitaires, can be played with reduced decks with fewer ranks and/or suits; reducing the number of suits should make the game even easier, although reducing the ranks is likely to make the game harder rather than easier.   Volume 4B of Donald E. Knuth's The Art of Computer Programming discusses a random subset variation he calls Late Binding Solitaire (problem 486, p. 364, 645-646): 18 cards are dealt randomly, and the player tries to reduce to one pile by normal Accordion rules.   He gives a win rate of 44.32% based on a sample of 10,000 deals.

Traditional Play

I have now incorporated an automatic solver for the traditional version of Accordion into the Accordion Virtuoso program. It makes every play possible (from left to right) after each card is dealt, and can either play slides in preference to leaps, or vice versa. I have run all of the daily deals (those numbered 1 to 86400, which are dealt randomly by the New Deal option based on the second of the day) with both options. When playing leaps if both plays are available for the same card, 37 deals out of 86400 were won (about 1 in 2335). When playing slides first, 56 deals were won (about 1 in 1543); four deals (2071, 23197, 75566, and 76541) were won with both options. Deal 76541 is shown below, with 31 of the cards playable at the start (9 have a leap/slide option).   If all available plays (with sweepers turned off) are made from left to right, the deal is won.

The easiest and hardest random deals

Computer searches for the deals with the fewest and most initial moves may prove a fruitful way to look for very hard and very easy deals; so far I have searched the first 15 million Virtuoso deals.  One of the easiest may be number 5538652, which has 43 playable cards at the start, shown above: all but two cards at the beginning can either play or be played on.  A number of examples turned up where fewer than 10 cards are playable at the start.  So far I have been unable to solve any of these by hand.   Mark Masten's solver has managed to solve them all, but its technique is impenetrable, jumping around to different parts of the tableau to make plays, and sometimes teetering on the brink of running out of moves.  So far the hardest deal by far for the solver is number 1991636 (below); this took about two hours (of clock time) to solve, with the program taking 11919 attempts and examining 1618439 positions before finding a solution.  This deal has only 9 playable cards at the start, only one in the first half of the deal.

For comparison, one of the deals with the fewest playable cards is 2844920, which has 8 playable cards at the start, only two in the first half of the deal.  This is the second-hardest deal I've found so far: the solver took around five minutes to solve this, taking 451 attempts and examining 225649 positions.

It's harder than you think to play poorly -- Accordion Misère

Misère is a French term often used to refer to games played with an reversed object of play (such as lowball poker or giveaway chess).  In this case, what happens if we try to block ourselves and finish with as many cards as possible?  So far the best I have managed is in 4471529, which has only 9 playable cards at the start.  I managed to block after only 10 plays (TS-1 4C-1 QD-1 2C-1 9D-1 3H-1 JD-1 QS-3 KH-3 9H-3), leaving 42 cards (the blue background indicates no more moves are available):

This article is copyright © 2024 by Michael Keller. All rights reserved.